题目内容
如图,在△ABC中,点D在AC上,DA=DB,∠C=∠DBC,以AB为直径的 交AC于点E,F是
交AC于点E,F是 上的点,且AF=BF.
上的点,且AF=BF.
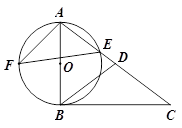
(1)求证:BC是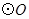 的切线;
的切线;
(2)若sinC=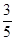 ,AE=
,AE=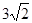 ,求sinF的值和AF的长.
,求sinF的值和AF的长.
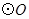 交AC于点E,F是
交AC于点E,F是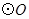 上的点,且AF=BF.
上的点,且AF=BF. 
(1)求证:BC是
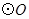 的切线;
的切线; (2)若sinC=
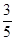 ,AE=
,AE=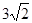 ,求sinF的值和AF的长.
,求sinF的值和AF的长.(1)证明:∵DA=DB,
∴∠DAB=∠DBA.
又∵∠C=∠DBC,
∴∠DBA﹢∠DBC=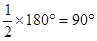 .
.
∴AB⊥BC.
又∵AB是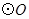 的直径,
的直径,
∴BC是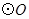 的切线.……………………………………2分
的切线.……………………………………2分
(2)解:如图,连接BE,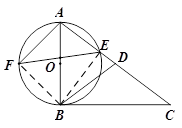
∵AB是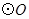 的直径,
的直径,
∴∠AEB=90°.
∴∠EBC+∠C=90°.
∵∠ABC=90°,
∴∠ABE+∠EBC=90°.
∴∠C=∠ABE.
又∵∠AFE=∠ABE,
∴∠AFE=∠C.
∴sin∠AFE=sin∠ABE=sinC.
∴sin∠AFE=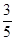 . ………………………………3分
. ………………………………3分
连接BF,
∴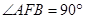 .
.
 在Rt△ABE中,
在Rt△ABE中,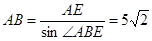 . …………………4分
. …………………4分
∵AF=BF,
∴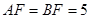 . ……………………………………5分
. ……………………………………5分
∴∠DAB=∠DBA.
又∵∠C=∠DBC,
∴∠DBA﹢∠DBC=
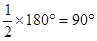 .
.∴AB⊥BC.
又∵AB是
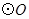 的直径,
的直径,∴BC是
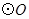 的切线.……………………………………2分
的切线.……………………………………2分(2)解:如图,连接BE,

∵AB是
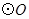 的直径,
的直径,∴∠AEB=90°.
∴∠EBC+∠C=90°.
∵∠ABC=90°,
∴∠ABE+∠EBC=90°.
∴∠C=∠ABE.
又∵∠AFE=∠ABE,
∴∠AFE=∠C.
∴sin∠AFE=sin∠ABE=sinC.
∴sin∠AFE=
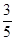 . ………………………………3分
. ………………………………3分连接BF,
∴
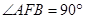 .
. 在Rt△ABE中,
在Rt△ABE中,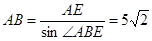 . …………………4分
. …………………4分∵AF=BF,
∴
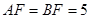 . ……………………………………5分
. ……………………………………5分(1)AB是直径.证明AB⊥BC即可.
(2)连接BE,证得∠AFE=∠C. 即可求出sinF的值,连接BF,通过解直角三角形ABE求得BF,即可
(2)连接BE,证得∠AFE=∠C. 即可求出sinF的值,连接BF,通过解直角三角形ABE求得BF,即可

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
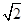 ≈1.414,
≈1.414,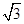 ≈1.732.最后结果精确到1米)
≈1.732.最后结果精确到1米)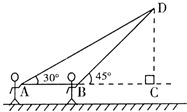
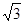 ︰2 B. 1︰3 C. 2︰3 D.
︰2 B. 1︰3 C. 2︰3 D. 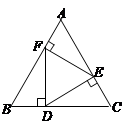
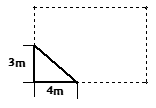
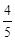 ,则坡面AC的长度为( )
,则坡面AC的长度为( )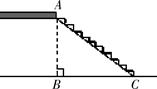
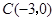 ,点
,点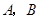 分别在
分别在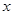 轴,
轴,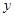 轴的正半轴上,且满足
轴的正半轴上,且满足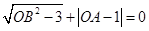 .
.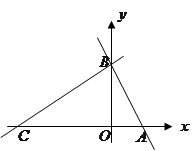
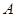 ,点
,点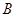 的坐标
的坐标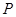 从
从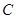 点出发,以每秒1个单位的速度沿线段
点出发,以每秒1个单位的速度沿线段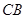 运动,连结
运动,连结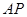 .设
.设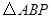 的面积为
的面积为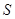 ,点
,点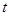 秒,求
秒,求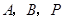 为顶点的三角形与
为顶点的三角形与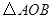 相似?若存在,请直接写出点
相似?若存在,请直接写出点 海里/小时
海里/小时 海里/小时
海里/小时 海里/小时
海里/小时 海里/小时
海里/小时