题目内容
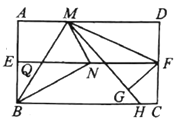
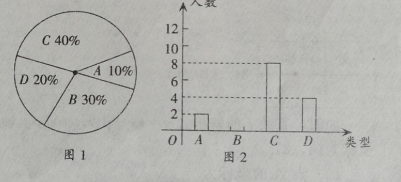
【题目】某校要求200名学生进行社会调查，每人必须完成3~6份报告，调查结束后随机抽查了20名学生每人完成报告的份数，并分为四类，A：3份；B：4份；C：5份；D：6份 各类的人数绘制成扇形图（如图1）和尚未完整的条形图（如图2），回答下列问题：
（1）请将条形统计图2补充完整；
（2）写出这20名学生每天完成报告份数的众数 份和中位数；
（3）在求出20名学生每人完成报告份数的平均数时，小明是这样分析的 第一步：求平均数的公式是
=
+
+
+…+
）
第二步：在该问题中，n=4 
=3， 
=4， 
=5 
=6
第三步
=
（3+4+5+6）=4.5（份）
小明的分析对不对？如果对，请说明理由，如果不对，请求出正确结果；
（4）现从“D类”的学生中随机选出2人进行采访，若“D类”的学生中只有1名 男生，则所选两位同学中有男同学的概率是多少？请用列表法或树状图的方法求解．
【答案】（1）答案见解析，6人；（2）5 5；（3）不对，正确结果为4.7；（4）
.
【解析】试题分析：（1）先求出B中的人数，作图即可，（2）利用中位数及众数的定义求解即可．
（3）利用加权平均数的定义求解，并运用求出的加权平均数求200名学生共完成报告的份数即可；
（4）列出表格，根据概率公式计算即可．
试题解析：解：（1）B中的人数为：20﹣2﹣8﹣4=6人，如图：
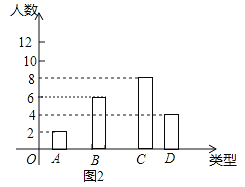
（2）这20名学生每天完成报告份数的众数5份和中位数5份；
故答案为：5，5．
（3）不对， 
=
=4.7份．
（4）设“D类”学生的编号为1，2，3，4，其中1号学生为男生，列表如下：
由表格可知：所有等可能的结果为12种，有男同学的结果为6种，∴P（有男同学）=
．
【题目】某公司计划投入50万元，开发并生产甲乙两种产品，根据市场调查预计甲产品的年获利y1（万元）与投入资金x（万元）成正比例，乙产品的年获利y2（万元）与投入资金x（万元）的平方成正比例，设该公司投入乙产品x（万元），两种产品的年总获利为y万元（x≥0），得到了表中的数据．
x（万元） | 20 | 30 |
y（万元） | 10 | 13 |
（1）求y与x的函数关系式；
（2）该公司至少可获得多少利润？请你利用所学的数学知识对该公司投入资金的分配提出合理化建
议，使他能获得最大利润，并求出最大利润是多少？
（3）若从年总利润扣除投入乙产品资金的a倍（a≤1）后，剩余利润随x增大而减小，求a的取值
范围．
