题目内容
【题目】如图,在等边△ABC中,AC=10,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是 ( )
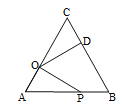
A. 5B. 6C. 7D. 9
【答案】C
【解析】
先计算出OC=7,根据等边三角形的性质得∠A=∠C=60°,再根据旋转的性质得OD=OP,∠POD=60°,根据三角形内角和和平角定义得∠1+∠2+∠A=180°,∠1+∠3+∠POD=180°,利用等量代换可得∠2=∠3,然后根据“AAS”判断△AOP≌△CDO,则AP=CO=7.
解:如图,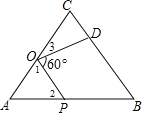
∵AC=10,AO=3,
∴OC=7,
∵△ABC为等边三角形,
∴∠A=∠C=60°,
∵线段OP绕点D逆时针旋转60゜得到线段OD,要使点D恰好落在BC上,
∴OD=OP,∠POD=60°,
∵∠1+∠2+∠A=180°,∠1+∠3+∠POD=180°,
∴∠1+∠2=120°,∠1+∠3=120°,
∴∠2=∠3,
在△AOP和△CDO中,
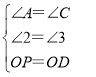
∴△AOP≌△CDO,
∴AP=CO=7,
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某淘宝商家计划平均每天销售某品牌儿童滑板车100辆,但由于种种原因,实际每天的销售量与计划量相比有出入。下表是某周的销售情况(超额记为正、不足记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 | +4 | -3 | -5 | +14 | -8 | +21 | -6 |
(1)根据记录的数据可知该店前三天共销售该品牌儿童滑板车______辆。
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售______辆。
(3)该店实行每日计件工资制,每销售一辆车可得40元,若超额完成任务,则超过部分每辆另奖15元;少销售一辆扣20元,那么该店铺的销售人员这一周的工资总额是多少元?