ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΉέΚœ”κ ΒΦυ
Ιέ≤λ≤¬œκ

»γΆΦ1Θ§”–ΙΪΙ≤÷±Ϋ«ΕΞΒψ![]() ΒΡΝΫΗω≤Μ»ΪΒ»ΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«≥ΏΒΰΖ≈‘Ύ“ΜΤπΘ§Βψ
ΒΡΝΫΗω≤Μ»ΪΒ»ΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«≥ΏΒΰΖ≈‘Ύ“ΜΤπΘ§Βψ![]() ‘Ύ
‘Ύ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘Ύ
‘Ύ![]() …œ.
…œ.
Θ®1Θ©‘ΎΆΦ1÷–Θ§ΡψΖΔœ÷œΏΕΈ![]() Θ§
Θ§![]() ΒΡ ΐΝΩΙΊœΒ «___________Θ§÷±œΏ
ΒΡ ΐΝΩΙΊœΒ «___________Θ§÷±œΏ![]() Θ§
Θ§![]() ΒΡΈΜ÷ΟΙΊœΒ «________.
ΒΡΈΜ÷ΟΙΊœΒ «________.
≤ΌΉςΖΔœ÷
Θ®2Θ©ΫΪΆΦ1÷–ΒΡ![]() »ΤΒψ
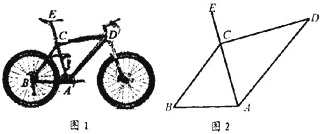
»ΤΒψ![]() Ρφ ±’κ–ΐΉΣ“ΜΗω»ώΫ«ΒΟΒΫΆΦ2Θ§’β ±Θ®1Θ©÷–ΒΡΝΫΗωΫα¬έ «Ζώ≥…ΝΔΘΩΉς≥ω≈–Εœ≤ΔΥΒΟςάμ”…ΘΜ
Ρφ ±’κ–ΐΉΣ“ΜΗω»ώΫ«ΒΟΒΫΆΦ2Θ§’β ±Θ®1Θ©÷–ΒΡΝΫΗωΫα¬έ «Ζώ≥…ΝΔΘΩΉς≥ω≈–Εœ≤ΔΥΒΟςάμ”…ΘΜ
ΆΊΙψΧΫΥς
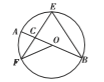
Θ®3Θ©»γΆΦ3Θ§»τ÷ΜΑ―ΓΑ”–ΙΪΙ≤÷±Ϋ«ΕΞΒψ![]() ΒΡΝΫΗω≤Μ»ΪΒ»ΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«≥ΏΓ±ΗΡΈΣΓΑ”–ΙΪΙ≤ΕΞΫ«ΈΣ
ΒΡΝΫΗω≤Μ»ΪΒ»ΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«≥ΏΓ±ΗΡΈΣΓΑ”–ΙΪΙ≤ΕΞΫ«ΈΣ![]() Θ®»ώΫ«Θ©ΒΡΝΫΗω≤Μ»Ϊ»»―ϋ»ΐΫ«–ΈΓ±Θ§
Θ®»ώΫ«Θ©ΒΡΝΫΗω≤Μ»Ϊ»»―ϋ»ΐΫ«–ΈΓ±Θ§![]() »ΤΒψ
»ΤΒψ![]() Ρφ ±’κ–ΐΉΣ»Έ“β“ΜΗω»ώΫ«Θ§’β ±Θ®1Θ©÷–ΒΡΝΫΗωΫα¬έ»‘»Μ≥…ΝΔ¬πΘΩΉς≥ω≈–ΕœΘ§≤Μ±ΊΥΒΟςάμ”….
Ρφ ±’κ–ΐΉΣ»Έ“β“ΜΗω»ώΫ«Θ§’β ±Θ®1Θ©÷–ΒΡΝΫΗωΫα¬έ»‘»Μ≥…ΝΔ¬πΘΩΉς≥ω≈–ΕœΘ§≤Μ±ΊΥΒΟςάμ”….
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§
Θ§![]() ΘΜΘ®2Θ©ΫΪΆΦ1÷–ΒΡ
ΘΜΘ®2Θ©ΫΪΆΦ1÷–ΒΡ![]() »ΤΒψ
»ΤΒψ![]() Ρφ ±’κ–ΐΉΣ“ΜΗω»ώΫ« ±Θ§ΝΫΗωΫα¬έ≥…ΝΔ.άμ”…ΦϊΫβΈωΘΜΘ®3Θ©Ϋα¬έ
Ρφ ±’κ–ΐΉΣ“ΜΗω»ώΫ« ±Θ§ΝΫΗωΫα¬έ≥…ΝΔ.άμ”…ΦϊΫβΈωΘΜΘ®3Θ©Ϋα¬έ![]() ≥…ΝΔΘΜΫα¬έ
≥…ΝΔΘΜΫα¬έ![]() ≤Μ≥…ΝΔ.
≤Μ≥…ΝΔ.
ΓΨΫβΈωΓΩ
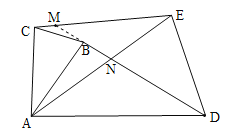
Θ®1Θ©ΗυΨίΓςABCΚΆΓςADE «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΒΟΒΫAB=ACΘ§AD=AEΘ§ΓœA=90ΓψΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
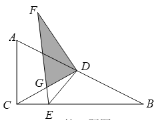
Θ®2Θ©”…–ΐΉΣΒΡ–‘÷ ΒΟΒΫΓœDAB=ΓœEACΘ°ΗυΨίSAS÷ΛΟςΓςABDΓ’ΓςACEΘ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡΕ‘”Π±ΏœύΒ»ΒΟ≥ωBD=CEΘ°―”≥ΛDBΘ§ΫΜCE”ΎΒψFΘ§ΫΜAE”ΎΒψOΘ°”…»ΪΒ»»ΐΫ«–ΈΕ‘”ΠΫ«œύΒ»ΒΟΒΫΓœADB=ΓœAECΘ°ΗυΨί»ΐΫ«–ΈΡΎΫ«ΚΆΕ®άμΚΆΕ‘ΕΞΫ«œύΒ»Θ§ΒΟΒΫΓœOFE=ΓœOAD=90ΓψΘ§Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
Θ®3Θ©άύΥΤΘ®2Θ©Ω…ΒΟBD=CE≥…ΝΔΘ§BDΓΆCE≤Μ≥…ΝΔΘ°
Θ®1Θ©ΓΏΓςABCΚΆΓςADE «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΓύAB=ACΘ§AD=AEΘ§ΓœA=90ΓψΘ§ΓύBD=CEΘ§BDΓΆCEΘ°
Ι ¥πΑΗΈΣΘΚBD=CEΘ§BDΓΆCEΘ°
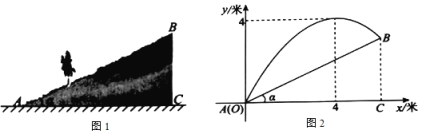
Θ®2Θ©ΫΪΆΦ1÷–ΒΡΓςABC»ΤΒψAΡφ ±’κ–ΐΉΣ“ΜΗω»ώΫ« ±Θ§ΝΫΗωΫα¬έ≥…ΝΔΘ°άμ”…»γœ¬ΘΚ
”…–ΐΉΣΒΟΘΚΓœDAB=ΓœEACΘ°
”÷ΓΏAB=ACΘ§AD=AEΘ§
ΓύΓςABDΓ’ΓςACEΘ®SASΘ©Θ°
ΓύBD=CEΘ°
»γΆΦΘ§―”≥ΛDBΘ§ΫΜCE”ΎΒψFΘ§ΫΜAE”ΎΒψOΘ°
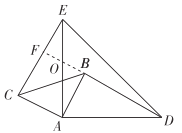
ΓΏΓςABDΓ’ΓςACEΘ§
ΓύΓœADB=ΓœAECΘ°
ΓΏΓœAOD=ΓœEOFΘ°
ΓύΓœOFE=ΓœOADΘ°
ΓΏΓœOAD=90ΓψΘ§
ΓύΓœDFE=90ΓψΘ§Φ¥BDΓΆCEΘ°
Θ®3Θ©Ϋα¬έBD=CE≥…ΝΔΘ§Ϋα¬έBDΓΆCE≤Μ≥…ΝΔΘ°άμ”…»γœ¬ΘΚ
”…–ΐΉΣΒΟΘΚΓœDAE=ΓœBACΘ§
ΓύΓœDAB=ΓœEACΘ°
”÷ΓΏAB=ACΘ§AD=AEΘ§
ΓύΓςABDΓ’ΓςACEΘ®SASΘ©Θ°
ΓύBD=CEΘ°
―”≥ΛDBΫΜCE”ΎMΘ§BD”κAEΫΜ”ΎΒψNΘ°
ΓΏΓςABDΓ’ΓςACEΘ§ΓύΓœMEA=ΓœBDAΘ°
ΓΏΓœENM=ΓœDNAΘ§ΓύΓœEMN=ΓœEADΘ°
ΓΏΓœEADΓΌ90ΓψΘ§ΓύΓœEMNΓΌ90ΓψΘ§ΓύBDΓΆCE≤Μ≥…ΝΔΘ°