题目内容
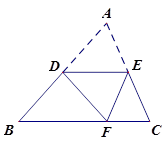
如图△ABC中,∠C=90º,∠A=30º,BC=5cm;△DEF中,∠D=90º,∠E=45º,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).
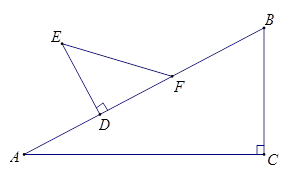
(1)在△DEF沿AB方向移动的过程中,有人发现:E、B两点间的距离随AD的变化而变化,现设AD="x,BE=y," 请你写出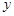 与
与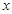 之间的函数关系式及其定义域.
之间的函数关系式及其定义域.
(2)请你进一步研究如下问题:
问题①:当△DEF移动至什么位置,即AD的长为多少时,E、B的连线与AC平行?
问题②:在△DEF的移动过程中,是否存在某个位置,使得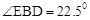 ?如果存在,求出AD的长度;如果不存在,请说明理由.
?如果存在,求出AD的长度;如果不存在,请说明理由.
问题③:当△DEF移动至什么位置,即AD的长为多少时,以线段AD、EB、BC的长度为三边长的三角形是直角三角形?

(1)在△DEF沿AB方向移动的过程中,有人发现:E、B两点间的距离随AD的变化而变化,现设AD="x,BE=y," 请你写出
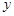 与
与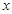 之间的函数关系式及其定义域.
之间的函数关系式及其定义域.(2)请你进一步研究如下问题:
问题①:当△DEF移动至什么位置,即AD的长为多少时,E、B的连线与AC平行?
问题②:在△DEF的移动过程中,是否存在某个位置,使得
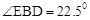 ?如果存在,求出AD的长度;如果不存在,请说明理由.
?如果存在,求出AD的长度;如果不存在,请说明理由.问题③:当△DEF移动至什么位置,即AD的长为多少时,以线段AD、EB、BC的长度为三边长的三角形是直角三角形?
(1)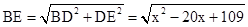 (其中0
(其中0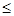 x
x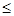 7)
7)
①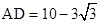 ,②
,②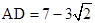 ,
,
③当AD为斜边时,AD =BE
=BE +BC
+BC ,
, =
=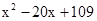 +25解得x=6.7
+25解得x=6.7
当BE为斜边时,BE =AD
=AD +BC
+BC ,
,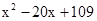 =
=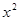 +25解得x=4.2
+25解得x=4.2
当BC为斜边时,BC =BE
=BE +AD
+AD ,25=
,25= +
+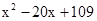 无实数解
无实数解
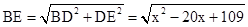 (其中0
(其中0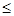 x
x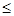 7)
7) ①
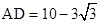 ,②
,②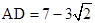 ,
,③当AD为斜边时,AD
 =BE
=BE +BC
+BC ,
, =
=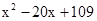 +25解得x=6.7
+25解得x=6.7当BE为斜边时,BE
 =AD
=AD +BC
+BC ,
,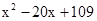 =
=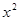 +25解得x=4.2
+25解得x=4.2当BC为斜边时,BC
 =BE
=BE +AD
+AD ,25=
,25= +
+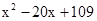 无实数解
无实数解试题分析:
(1)根据题意,观察图形,由勾股定理即可求出;
(2)①因为∠B=90°,∠A=30°,BC=5cm,所以AC=10cm,又因为∠FDE=90°,∠DEF=45°,DE=3cm,连接BE,设BE∥AC,则可求证∠FCD=∠A=30°,故AD的长可求;
②假设∠EBD=22.5°,因为∠EDF=45°,所以EF=BF,求得AD=
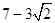 ,故不存在.
,故不存在.③设AD=x,则BE=
 ,再分情况讨论:FC为斜边;AD为斜边;BC为斜边.综合分析即可求得AD的长;
,再分情况讨论:FC为斜边;AD为斜边;BC为斜边.综合分析即可求得AD的长;试题解析:
∵△ABC中,∠C=90°,∠A=30°,BC=5,
∴AB=10
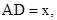
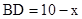 ,
,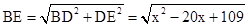 (其中0
(其中0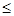 x
x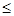 7)
7)(2)①当BE∥AC时,则∠EBD=∠A=30°
∴
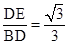 ,
,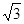
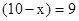 ,∴
,∴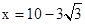
②当∠EBD=22.5°,∵∠EFD=45°,∴EF=BF,
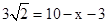 ,∴
,∴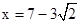
③
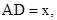 BE=
BE= ,BC="5"
,BC="5" 当AD为斜边时,AD
 =BE
=BE +BC
+BC ,
, =
=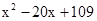 +25解得x=6.7
+25解得x=6.7当BE为斜边时,BE
 =AD
=AD +BC
+BC ,
,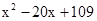 =
=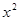 +25解得x=4.2
+25解得x=4.2当BC为斜边时,BC
 =BE
=BE +AD
+AD ,25=
,25= +
+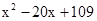 无实数解
无实数解
练习册系列答案
相关题目
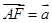 ,
, .
.
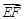 、
、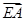 (用向量
(用向量 、
、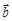 表示);
表示);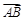 、
、 方向上的分向量.
方向上的分向量.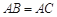 ,
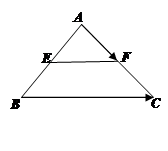
,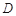 是
是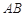 上一点,
上一点,  于点
于点 ,
,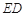 的延长线交
的延长线交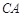 的延长线于点
的延长线于点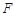 .求证:
.求证: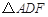 是等腰三角形.
是等腰三角形.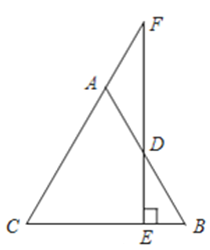
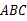 中,若三边长分别为9、12、15,则以两个这样的三角形拼成的长方形的面积为________.
中,若三边长分别为9、12、15,则以两个这样的三角形拼成的长方形的面积为________.