题目内容
如图,抛物线y=-2x2+bx与x轴的两个不同交点是O与A,顶点B在直线y=x上.
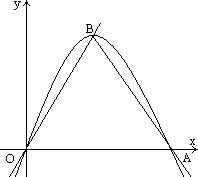
(1)求抛物线的解析式;
(2)证明△OAB是等边三角形;
(3)在抛物线上是否存在点P,使∠OPA=90°?若存在,请求出点P的坐标;若不存在,请说明理由,(抛物线y=ax2+bx+c的顶点坐标是(-![]() ,
,![]() )
)
答案:
解析:
解析:
|
(1)∵y=-2x2+bx的顶点坐标是B (2)抛物线y=-2x2+2 (3)解法一:假设存在符合条件的点P(m,n),依题意由图可知m>0,n>0,连结OP,PA,过点P作PD⊥OA于D,则Rt△OPD∽Rt△PAD,∴ 解法二:假高存在符合条件的点P(x,-2x2+2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ,且点B在直线y=
,且点B在直线y= .过B作BC⊥OA于C,则OC=
.过B作BC⊥OA于C,则OC= ,AB=
,AB= .∵OA=AB=BO=
.∵OA=AB=BO=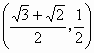 或P
或P

 ,求当△PON的面积最大时tan
,求当△PON的面积最大时tan
 的两根,且sin∠OBC=
的两根,且sin∠OBC= .
.
 :y=ax2+bx+1的顶点坐标为D(1,0),
:y=ax2+bx+1的顶点坐标为D(1,0),
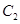 ,直线
,直线 ,
, 至点
至点 之间的一动点,
之间的一动点, 并延长交
并延长交 于点
于点 ,试问:当点Q运动到什么位置时,△BCF的面积为
,试问:当点Q运动到什么位置时,△BCF的面积为 。
。 ,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高.
,AO⊥BO.D为线段MN的中点,OH为Rt△OPC斜边上的高. 点的三角形与△AOB相似?若不存在,说明理由;若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由);并进一步探索对符合条件的每一个E点,直线NE与直线AB的交点G是否总满足PB·PG<
点的三角形与△AOB相似?若不存在,说明理由;若存在,求所有符合条件的抛物线的解析式,同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由);并进一步探索对符合条件的每一个E点,直线NE与直线AB的交点G是否总满足PB·PG< ,写出探索过程.
,写出探索过程.