题目内容
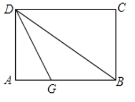
【题目】如图,直线AB:y=-x-b分别与x、y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于点C,且OB:OC=3:1.
(1)求直线BC的解析式;
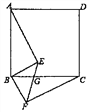
(2)如图,P为A点右侧x轴上的一动点,以P为直角顶点,BP为腰在第一象限内作等腰直角△BPQ,连接QA并延长交y轴于点K,当P点运动时,K点的位置是否发现变化?若不变,请求出它的坐标;如果变化,请说明理由.

【答案】(1)y=3x+6(2)K点的位置不发生变化,K(0,6),理由见解析
【解析】
(1)设BC的解析式是y=ax+c,由直线AB:y=xb过A(6,0),可以求出b,因此可以求出B点的坐标,再由已知条件可求出C点的坐标,把B,C点的坐标分别代入求出a和c的值即可;
(2)过Q作QH⊥x轴于H,首先证明△BOP≌△PHQ,再分别证明△AHQ和△AOK为等腰直角三角形,问题得解.
(1)由已知:0=6b,
∴b=6,
∴AB:y=x+6.
∴B(0,6),
∴OB=6,
∵OB:OC=3:1,
OC=![]() =2,
=2,
∴C(2,0),
设BC的解析式是y=ax+c,代入得![]() ,
,
解得:![]() ,
,
∴直线BC的解析式是:y=3x+6;
(2)K点的位置不发生变化,K(0,6).
过Q作QH⊥x轴于H,
∵△BPQ是等腰直角三角形,
∴∠BPQ=90°,PB=PQ,
∵∠BOA=∠QHA=90°,
∴∠BPO=∠PQH,
∴△BOP≌△PHQ,
∴PH=BO,OP=QH,
∴PH+PO=BO+QH,
即OA+AH=BO+QH,
又OA=OB,
∴AH=QH,
∴△AHQ是等腰直角三角形,
∴∠QAH=45°,
∴∠OAK=45°,
∴△AOK为等腰直角三角形,
∴OK=OA=6,
∴K(0,6).


练习册系列答案
相关题目