题目内容
【题目】如图,直线y=3x与双曲线y= ![]() (k≠0,且x>0)交于点A,点A的横坐标是1.
(k≠0,且x>0)交于点A,点A的横坐标是1.
(1)求点A的坐标及双曲线的解析式;
(2)点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.
【答案】
(1)解:将x=1代入y=3x,得:y=3,
∴点A的坐标为(1,3),将A(1,3)代入 ![]() ,得:k=3,
,得:k=3,
∴反比例函数的解析式为 ![]() ;
;
(2)解:在 ![]() 中y=1时,x=3,
中y=1时,x=3,
∴点B(3,1),如图,S△AOB=S矩形OCED﹣S△AOC﹣S△BOD﹣S△ABE=3×3﹣ ![]() ×1×3﹣
×1×3﹣ ![]() ×1×3﹣
×1×3﹣ ![]() ×2×2=4.
×2×2=4.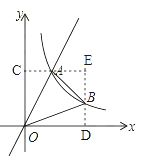
【解析】(1)根据点A的横坐标是1及点A在直线y=3x,可求出点A的坐标;再根据点A的坐标,利用待定系数法求出双曲线的解析式即可。
(2)根据点B的纵坐标是1.将y=1代入双曲线的解析式求出点B的横坐标,再根据S△AOB=S矩形OCED﹣S△AOC﹣S△BOD﹣S△ABE , 计算即可得出答案。

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】从甲地到乙地有![]() 三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时的频数 公交车用时线路 |
|
|
|
| 合计 |
| 59 | 151 | 166 | 124 | 500 |
| 50 | 50 | 122 | 278 | 500 |
| 45 | 265 | 160 | 30 | 500 |
早高峰期间,乘坐_________(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
【题目】超市为减小![]() 商品的积压,决定采取降价销售的策略,若某商品的原价为
商品的积压,决定采取降价销售的策略,若某商品的原价为![]() 元,随着不同幅度的降价,日销量(单位为件)发生相应的变化如表:
元,随着不同幅度的降价,日销量(单位为件)发生相应的变化如表:
降价(元) |
|
|
|
|
|
|
日销量(件) |
|
|
|
|
|
|
![]() 这个表反映了________ 和________ 两个变量之间的关系;
这个表反映了________ 和________ 两个变量之间的关系;
![]() 从表中可以看出每降价
从表中可以看出每降价![]() 元,日销量增加_ 件;
元,日销量增加_ 件;
![]() 可以估计降价之前的日销量为_ _件;
可以估计降价之前的日销量为_ _件;
![]() 设日销量为
设日销量为![]() 件,降价为
件,降价为![]() 元,由上表呈现的规律,猜想
元,由上表呈现的规律,猜想![]() 与
与![]() 的函数关系式为_
的函数关系式为_
![]() 当售价为
当售价为![]() 元时,日销量为 ________件.
元时,日销量为 ________件.
【题目】某生物课外活动小组的同学进行植物标本制作比赛,结果统计如下表:
每人所制 作标本数 | 2 | 4 | 6 | 8 | 10 |
人数 | 1 | 2 | 4 | 3 | 2 |
请根据表中信息,回答下列问题:
(1)该活动小组共有学生多少人?
(2)制作标本数在6个及以上的人数占小组总人数的百分比是多少?
(3)根据统计表制作一个合适的统计图来描述这次比赛的结果.