题目内容
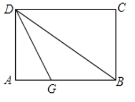
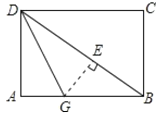
【题目】如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,再折叠使AD边与BD重合,得折痕DG,若AB=4,BC=3,求AG的长.
【答案】![]()
【解析】
过点G作GE⊥BD于E,由折叠长方形纸片ABCD,先折出折痕(对角线)BD,再折叠使AD边与BD重合,得折痕DG,即可得:∠GDA=∠GDB,AD=ED,因为GE⊥BD,AG=EG,设AG=x,则GE=x,BE=BDDE=53=2,BG=ABAG=4x,在Rt△BEG中利用勾股定理,即可求得AG的长.
过点G作GE⊥BD于E,
根据题意可得:∠GDA=∠GDB,AD=ED,
∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=3,
∴AG=EG,ED=3,
∵AB=4,BC=3,∠A=90°,
∴BD=5,
设AG=x,则GE=x,BE=BDDE=53=2,BG=ABAG=4x,
在Rt△BEG中,EG2+BE2=BG2,
即:x2+22=(4x)2,
解得:x=![]() ,
,
故AG=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】超市为减小![]() 商品的积压,决定采取降价销售的策略,若某商品的原价为
商品的积压,决定采取降价销售的策略,若某商品的原价为![]() 元,随着不同幅度的降价,日销量(单位为件)发生相应的变化如表:
元,随着不同幅度的降价,日销量(单位为件)发生相应的变化如表:
降价(元) |
|
|
|
|
|
|
日销量(件) |
|
|
|
|
|
|
![]() 这个表反映了________ 和________ 两个变量之间的关系;
这个表反映了________ 和________ 两个变量之间的关系;
![]() 从表中可以看出每降价
从表中可以看出每降价![]() 元,日销量增加_ 件;
元,日销量增加_ 件;
![]() 可以估计降价之前的日销量为_ _件;
可以估计降价之前的日销量为_ _件;
![]() 设日销量为
设日销量为![]() 件,降价为
件,降价为![]() 元,由上表呈现的规律,猜想
元,由上表呈现的规律,猜想![]() 与
与![]() 的函数关系式为_
的函数关系式为_
![]() 当售价为
当售价为![]() 元时,日销量为 ________件.
元时,日销量为 ________件.