题目内容
【题目】已知在![]() 中,
中, ![]() ,以
,以![]() 上的一点
上的一点![]() 为圆心,以
为圆心,以![]() 为半径的圆交
为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.

(![]() )求证:
)求证: ![]() .
.
(![]() )如果
)如果![]() 是⊙
是⊙![]() 的切线,
的切线, ![]() 是切点,
是切点, ![]() 是
是![]() 的中点,当
的中点,当![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)AC=4.
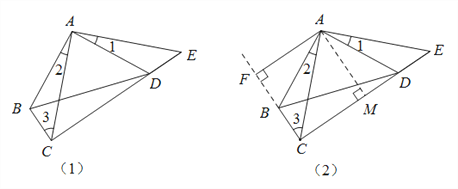
【解析】试题分析:(1)连接DE,根据圆周角定理求得∠ADE=90°,得出∠ADE=∠ABC,进而证得△ADE∽△ABC,根据相似三角形对应边成比例即可求得结论;
(2)连接OD,根据切线的性质求得OD⊥BD,在RT△OBD中,根据已知求得∠OBD=30°,进而求得∠BAC=30°,根据30°的直角三角形的性质即可求得AC的长.
试题解析:(1)证明:连接DE,∵AE是直径,∴∠ADE=90°,∴∠ADE=∠ABC,∵∠DAE=∠BAC,∴△ADE∽△ABC,∴ ![]() ,∴ACAD=ABAE;
,∴ACAD=ABAE;
(2)解:连接OD,∵BD是⊙O的切线,∴OD⊥BD,在RT△OBD中,OE=BE=OD,∴OB=2OD,∴∠OBD=30°,同理∠BAC=30°,在RT△ABC中,AC=2BC=2×2=4.


练习册系列答案
相关题目