题目内容
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(![]() )求抛物线的解析式.
)求抛物线的解析式.
(![]() )设抛物线的顶点为
)设抛物线的顶点为![]() ,点
,点![]() 在抛物线的对称轴上,且
在抛物线的对称轴上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(![]() )点
)点![]() 在直线
在直线![]() 上方的抛物线上,是否存在点
上方的抛物线上,是否存在点![]() 使
使![]() 的面积最大,若存在,请求出点
的面积最大,若存在,请求出点![]() 坐标.
坐标.

【答案】(![]() )
)![]() (
(![]() )
)![]()
![]() 或
或![]() (
(![]() )存在,
)存在, ![]()
![]() .
.
【解析】试题分析:(1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数的值;
(2)根据(1)得到的函数解析式,可求出D、C的坐标;易证得△OBC是等腰Rt△,若过A作BC的垂线,设垂足为E,在Rt△ABE中,根据∠ABE的度数及AB的长即可求出AE、BE、CE的长;连接AC,设抛物线的对称轴与x轴的交点为F,若∠APD=∠ACB,那么△AEC与△AFP,根据得到的比例线段,即可求出PF的长,也就求得了P点的坐标;
(3)当Q到直线BC的距离最远时,△QBC的面积最大(因为BC是定长),可过Q作y轴的平行线,交BC于S;根据B、C的坐标,易求出直线BC的解析式,可设出Q点的坐标,根据抛物线和直线BC的解析式,分别表示出Q、S的纵坐标,即可得到关于QS的长以及Q点横坐标的函数关系式,以QS为底,B、C横坐标差的绝对值为高可得到△QBC的面积,由于B、C横坐标差的绝对值为定值,那么QS最长时,△QBC的面积最大,此时Q离BC的距离最远;可根据上面得到的函数的性质求出QS的最大值及对应的Q点横坐标,然后将其代入抛物线的解析式中,即可求出Q点的坐标.
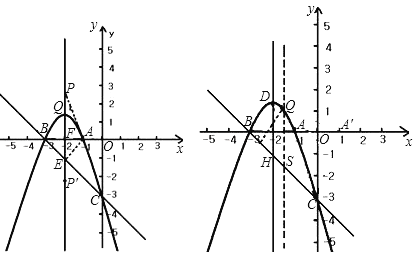
试题解析:解:(1)∵抛物线y=﹣x2+bx+c经过A(﹣1,0),B(﹣3,0),∴![]() ,
,
解得: ![]() ,∴抛物线的解析式为y=﹣x2﹣4x﹣3;
,∴抛物线的解析式为y=﹣x2﹣4x﹣3;
(2)由y=﹣x2﹣4x﹣3,可得D(﹣2,1),C(0,﹣3),∴OB=3,OC=3,OA=1,AB=2,可得△OBC是等腰直角三角形,∴∠OBC=45°,CB=![]() ,如图,设抛物线对称轴与x轴交于点F,∴AF=
,如图,设抛物线对称轴与x轴交于点F,∴AF=![]() AB=1,过点A作AE⊥BC于点E,∴∠AEB=90°,可得BE=AE=
AB=1,过点A作AE⊥BC于点E,∴∠AEB=90°,可得BE=AE=![]() ,CE=
,CE=![]() ,在△AEC与△AFP中,∠AEC=∠AFP=90°,∠ACE=∠APF,∴△AEC∽△AFP,∴
,在△AEC与△AFP中,∠AEC=∠AFP=90°,∠ACE=∠APF,∴△AEC∽△AFP,∴![]() ,
, ![]() ,解得PF=2,∵点P在抛物线的对称轴上,∴点P的坐标为(﹣2,2)或(﹣2,﹣2);
,解得PF=2,∵点P在抛物线的对称轴上,∴点P的坐标为(﹣2,2)或(﹣2,﹣2);
(3)存在,因为BC为定值,当点Q到直线BC的距离最远时,△BCQ的面积最大,设直线BC的解析式y=kx+b,直线BC经过B(﹣3,0),C(0,﹣3),∴![]() ,
,
解得:k=﹣1,b=﹣3,∴直线BC的解析式y=﹣x﹣3,设点Q(m,n),过点Q作QH⊥BC于H,并过点Q作QS∥y轴交直线BC于点S,则S点坐标为(m,﹣m﹣3),∴QS=n﹣(﹣m﹣3)=n+m+3,∵点Q(m,n)在抛物线y=﹣x2﹣4x﹣3上,∴n=﹣m2﹣4m﹣3,∴QS=﹣m2﹣4m﹣3+m+3=﹣m2﹣3m=﹣(m+![]() )2+
)2+![]() ,当m=﹣
,当m=﹣![]() 时,QS有最大值
时,QS有最大值![]() ,∵BO=OC,∠BOC=90°,∴∠OCB=45°.
,∵BO=OC,∠BOC=90°,∴∠OCB=45°.
∵QS∥y轴,∴∠QSH=45°,∴△QHS是等腰直角三角形,∴当斜边QS最大时QH最大,∵当m=﹣![]() 时,QS最大,∴此时n=﹣m2﹣4m﹣3=﹣
时,QS最大,∴此时n=﹣m2﹣4m﹣3=﹣![]() +6﹣3=
+6﹣3=![]() ,∴Q(﹣
,∴Q(﹣![]() ,
, ![]() ),∴Q点的坐标为(﹣
),∴Q点的坐标为(﹣![]() ,
, ![]() )时,△BCQ的面积最大.
)时,△BCQ的面积最大.

 阅读快车系列答案
阅读快车系列答案