题目内容
如图,Rt△AOB是一张放在平面直角坐标系中的三角形纸片,点O与原点重合,点A在x轴正半轴上,点B在y轴正半轴上,OB=2 ,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE。
,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE。
(1)求点E和点D的坐标;
(2)求经过O、D、A三点的二次函数图像的解析式。
 ,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE。
,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE。 (1)求点E和点D的坐标;
(2)求经过O、D、A三点的二次函数图像的解析式。
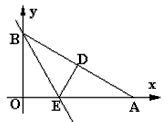
解:(1)过点D作DF⊥OA,垂足为F,因为Rt△AOB沿BE折叠时,OB边落在AB边上,点O与点D重合
所以,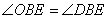 ,
,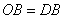
在Rt△AOB中,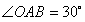 ∴
∴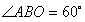
又∵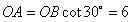 ,∴
,∴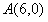
在Rt△AOB中,∵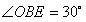 ,∴
,∴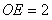 ∴
∴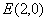
在Rt△AOB中,∵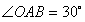 ∴
∴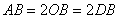
∴D是AB的中点,∴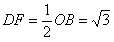 ,
,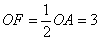 ∴
∴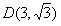
(2)设经过O、D、A三点的二次函数图像的解析式为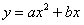 ,把
,把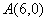 ,
,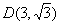 代入
代入
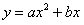 得
得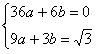 解得
解得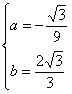
所以,经过O、D、A三点的二次函数图像的解析式为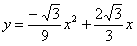 。
。
所以,
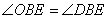 ,
,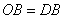
在Rt△AOB中,
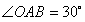 ∴
∴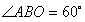
又∵
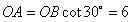 ,∴
,∴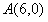
在Rt△AOB中,∵
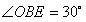 ,∴
,∴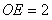 ∴
∴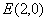
在Rt△AOB中,∵
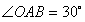 ∴
∴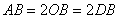
∴D是AB的中点,∴
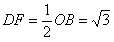 ,
,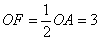 ∴
∴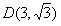
(2)设经过O、D、A三点的二次函数图像的解析式为
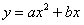 ,把
,把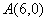 ,
,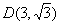 代入
代入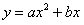 得
得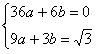 解得
解得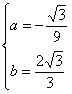
所以,经过O、D、A三点的二次函数图像的解析式为
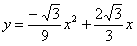 。
。
练习册系列答案
相关题目
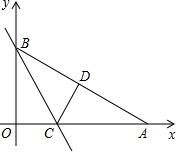 如图,Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上,OB=
如图,Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上,OB=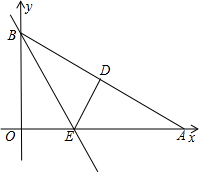 痕为BE.
痕为BE.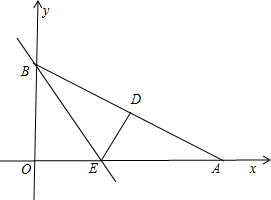 重合,点A在x轴上,点B在y轴上
重合,点A在x轴上,点B在y轴上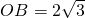 ,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折
,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折 痕为BE.
痕为BE. ,∠BAO=30度,将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC。
,∠BAO=30度,将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC。