题目内容
【题目】在四边形![]() 中,
中, ![]() ,对角线
,对角线![]() 平分
平分![]() .
.
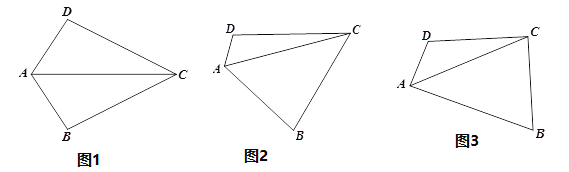
(1)如图1,若![]() ,且
,且![]() ,试探究边
,试探究边![]() 、
、![]() 与对角线
与对角线![]() 的数量关系并说明理由.
的数量关系并说明理由.
(2)如图2,若将(1)中的条件“![]() ”去掉,(1)中的结论是否成立?请说明理由.
”去掉,(1)中的结论是否成立?请说明理由.
(3)如图3,若![]() ,探究边
,探究边![]() 、
、![]() 与对角线
与对角线![]() 的数量关系并说明理由.
的数量关系并说明理由.
【答案】(1)![]() .证明见解析;(2)成立;(3)
.证明见解析;(2)成立;(3)![]() .理由见解析.
.理由见解析.
【解析】试题分析:(1)结论:AC=AD+AB,只要证明AD=![]() AC,AB=
AC,AB=![]() AC即可解决问题;
AC即可解决问题;
(2)(1)中的结论成立.以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,只要证明△DAC≌△BEC即可解决问题;
(3)结论:AD+AB=![]() AC.过点C作CE⊥AC交AB的延长线于点E,只要证明△ACE是等腰直角三角形,△DAC≌△BEC即可解决问题;
AC.过点C作CE⊥AC交AB的延长线于点E,只要证明△ACE是等腰直角三角形,△DAC≌△BEC即可解决问题;
试题解析:解:(1)AC=AD+AB.
理由如下:如图1中,
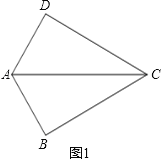
在四边形ABCD中,∠D+∠B=180°,∠B=90°,
∴∠D=90°,
∵∠DAB=120°,AC平分∠DAB,
∴∠DAC=∠BAC=60°,
∵∠B=90°,
∴AB=![]() AC,同理AD=
AC,同理AD=![]() AC.
AC.
∴AC=AD+AB.
(2)(1)中的结论成立,理由如下:以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,
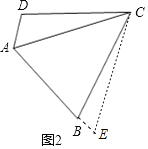
∵∠BAC=60°,
∴△AEC为等边三角形,
∴AC=AE=CE,
∵∠D+∠ABC=180°,∠DAB=120°,
∴∠DCB=60°,
∴∠DCA=∠BCE,
∵∠D+∠ABC=180°,∠ABC+∠EBC=180°,
∴∠D=∠CBE,∵CA=CE,
∴△DAC≌△BEC,
∴AD=BE,
∴AC=AD+AB.
(3)结论:AD+AB=![]() AC.理由如下:
AC.理由如下:
过点C作CE⊥AC交AB的延长线于点E,∵∠D+∠B=180°,∠DAB=90°,
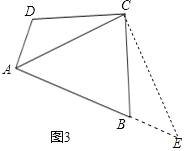
∴DCB=90°,
∵∠ACE=90°,
∴∠DCA=∠BCE,
又∵AC平分∠DAB,
∴∠CAB=45°,
∴∠E=45°.
∴AC=CE.
又∵∠D+∠ABC=180°,∠D=∠CBE,
∴△CDA≌△CBE,
∴AD=BE,
∴AD+AB=AE.
在Rt△ACE中,∠CAB=45°,
∴AE=![]()
∴![]() .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | |
乙 | 8 | 8 | 2.2 |
丙 | 6 | 3 |
(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定.求甲、乙相邻出场的概率.