题目内容
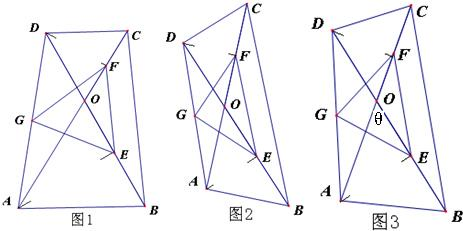
如图,线段AC与BD交于O,DO=DC,AO=AB,E,F,G分别是OB,OC,AD中点(1)如图1,当∠AOB=60°时,EG与FG的数量关系是
如图2,当∠AOB=45°时,EG与FG的数量关系是
(2)如图3,当∠AOB=θ时,EG与FG的数量关系是
(3)请你从上述三个结论中选择一个结论加以证明
分析:(1)由DO=DC,AO=AB,∠DOC=∠AOB=60°,可得:△DOC与△AOB是等边三角形,由三线合一可得DF⊥AC,AE⊥BD,又由直角三角形斜边上的中线是斜边的一半,可得EG=FG,又由DG=GF=AG=EG=
AD,利用等边对等角,即可求得∠FGE的度数;∠AOB=45°时,方法一样;
(2)与(1)的方法类似,注意此时△DOC与△AOB是等腰三角形,由等腰三角形中的三线合一仍可求得结果.
(3)根据以上分析证明即可.
| 1 |
| 2 |
(2)与(1)的方法类似,注意此时△DOC与△AOB是等腰三角形,由等腰三角形中的三线合一仍可求得结果.
(3)根据以上分析证明即可.
解答:解:(1)当∠AOB=60°时,
证明:连接DF与EG,
∵DO=DC,AO=AB,
∵∠DOC=∠AOB=60°,
∴△DOC与△AOB是等边三角形,
∵E,F,G分别是OB,OC,AD中点,
∴DF⊥AC,AE⊥BD,
∴EG=
AD,FG=
AD,
∴EG=FG,
∵∠DCO=∠BAO=60°,
∴AB∥CD,
∴∠CDA+∠DAB=180°,
∵∠CDO=
∠CDA=∠OAB=
BAO=30°,
∴∠ADF+∠EAG=120°,
∵DG=GF=AG=EG=
AD,
∴∠DFG=∠GDF,∠AEG=∠GAE,
∴∠DFG+∠AEG=∠ADF+∠EAG=120°,
∴∠DFG+∠AEG+∠ADF+∠EAG=240°,
∴∠DGF+∠AGE=360°-(∠DFG+∠AEG+∠ADF+∠EAG)=120°,
∴∠FGE=60°;
当∠AOB=45°时,
证明:连接DF与EG,
∵DO=DC,AO=AB,
∵∠DOC=∠AOB=45°,
∴△DOC与△AOB是等腰直角三角形,
∵E,F,G分别是OB,OC,AD中点,
∴DF⊥AC,AE⊥BD,
∴EG=
AD,FG=
AD,
∴EG=FG,
∵∠DCO=∠BAE=45°,
∴AE∥CD,
∴∠CDA+∠DAE=180°,
∵∠CDO=
∠CDO=∠OAB=
BAO=45°,
∴∠ADF+∠EAG=135°,
∵DG=GF=AG=EG=
AD,
∴∠DFG=∠GDF,∠AEG=∠GAE,
∴∠DFG+∠AEG=∠ADF+∠EAG=135°,
∴∠DFG+∠AEG+∠ADF+∠EAG=270°,
∴∠DGF+∠AGE=360°-(∠DFG+∠AEG+∠ADF+∠EAG)=190°,
∴∠FGE=90°;
(2)当∠AOB=θ时,
证明:连接DF与AE,
∵DO=DC,AO=AB,∵∠DOC=∠AOB=∠DCO=∠ABO=θ,
∴△DOC与△AOB是等腰三角形,
∵E,F,G分别是OB,OC,AD中点,
∴DF⊥AC,AE⊥BD,
∴EG=
AD,FG=
AD,
∴EG=FG,
∵∠FDO=∠EAO=90°-θ,
∴∠ODA+∠OAD=θ,
∴∠FDA+∠EAD=180°-θ,
∵DG=GF=AG=EG=
AD,
∴∠DFG=∠GDF,∠AEG=∠GAE,
∴∠DFG+∠AEG=∠ADF+∠EAG=180°-θ,
∴∠DFG+∠AEG+∠ADF+∠EAG=360°-2θ,
∴∠DGF+∠AGE=360°-(∠DFG+∠AEG+∠ADF+∠EAG)=180°-2θ,
∴∠FGE=180°-2θ.
故答案为:(1)EG=FG,60°; EG=FG,90°;
(2)EG=FG,180°-2θ;
(3)选择证明即可.
证明:连接DF与EG,
∵DO=DC,AO=AB,
∵∠DOC=∠AOB=60°,
∴△DOC与△AOB是等边三角形,
∵E,F,G分别是OB,OC,AD中点,
∴DF⊥AC,AE⊥BD,
∴EG=
| 1 |
| 2 |
| 1 |
| 2 |
∴EG=FG,
∵∠DCO=∠BAO=60°,
∴AB∥CD,
∴∠CDA+∠DAB=180°,
∵∠CDO=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ADF+∠EAG=120°,
∵DG=GF=AG=EG=
| 1 |
| 2 |
∴∠DFG=∠GDF,∠AEG=∠GAE,
∴∠DFG+∠AEG=∠ADF+∠EAG=120°,
∴∠DFG+∠AEG+∠ADF+∠EAG=240°,
∴∠DGF+∠AGE=360°-(∠DFG+∠AEG+∠ADF+∠EAG)=120°,
∴∠FGE=60°;
当∠AOB=45°时,
证明:连接DF与EG,
∵DO=DC,AO=AB,
∵∠DOC=∠AOB=45°,
∴△DOC与△AOB是等腰直角三角形,
∵E,F,G分别是OB,OC,AD中点,
∴DF⊥AC,AE⊥BD,
∴EG=
| 1 |
| 2 |
| 1 |
| 2 |
∴EG=FG,
∵∠DCO=∠BAE=45°,
∴AE∥CD,
∴∠CDA+∠DAE=180°,
∵∠CDO=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ADF+∠EAG=135°,
∵DG=GF=AG=EG=
| 1 |
| 2 |
∴∠DFG=∠GDF,∠AEG=∠GAE,
∴∠DFG+∠AEG=∠ADF+∠EAG=135°,
∴∠DFG+∠AEG+∠ADF+∠EAG=270°,
∴∠DGF+∠AGE=360°-(∠DFG+∠AEG+∠ADF+∠EAG)=190°,
∴∠FGE=90°;
(2)当∠AOB=θ时,
证明:连接DF与AE,
∵DO=DC,AO=AB,∵∠DOC=∠AOB=∠DCO=∠ABO=θ,
∴△DOC与△AOB是等腰三角形,
∵E,F,G分别是OB,OC,AD中点,
∴DF⊥AC,AE⊥BD,
∴EG=
| 1 |
| 2 |
| 1 |
| 2 |
∴EG=FG,
∵∠FDO=∠EAO=90°-θ,
∴∠ODA+∠OAD=θ,
∴∠FDA+∠EAD=180°-θ,
∵DG=GF=AG=EG=
| 1 |
| 2 |
∴∠DFG=∠GDF,∠AEG=∠GAE,
∴∠DFG+∠AEG=∠ADF+∠EAG=180°-θ,
∴∠DFG+∠AEG+∠ADF+∠EAG=360°-2θ,
∴∠DGF+∠AGE=360°-(∠DFG+∠AEG+∠ADF+∠EAG)=180°-2θ,
∴∠FGE=180°-2θ.
故答案为:(1)EG=FG,60°; EG=FG,90°;
(2)EG=FG,180°-2θ;
(3)选择证明即可.
点评:此题考查了三角形中位线的性质,直角三角形的性质以及等腰三角形的性质等知识.题目难度适中,注意数形结合思想的应用.

练习册系列答案
相关题目
 11、如图,线段AC与BD交于点O,且OA=OC,请添加一个条件,使△OAB≌△OCD,这个条件是
11、如图,线段AC与BD交于点O,且OA=OC,请添加一个条件,使△OAB≌△OCD,这个条件是 13、如图:线段AC与BD交于点O,且OA=OC,要使△OAB≌△OCD,需增添一个条件,你增加的条件为
13、如图:线段AC与BD交于点O,且OA=OC,要使△OAB≌△OCD,需增添一个条件,你增加的条件为 如图,线段AC与BD相交于点O,且OA=OC,请添加一个条件,使△OAB≌△OCD,这个条件可以是( )
如图,线段AC与BD相交于点O,且OA=OC,请添加一个条件,使△OAB≌△OCD,这个条件可以是( ) (2011•安宁市一模)下列语句叙述错误的个数是( )
(2011•安宁市一模)下列语句叙述错误的个数是( )