题目内容
【题目】已知:等腰三角形ABC的面积为30![]() ,AB=AC= 10
,AB=AC= 10![]() ,则底边BC的长度为_________ m.
,则底边BC的长度为_________ m.
【答案】![]() 或
或![]()
【解析】
作CD⊥AB于D,则∠ADC=∠BDC=90°,由三角形的面积求出CD,由勾股定理求出AD;分两种情况:①等腰△ABC为锐角三角形时,求出BD,由勾股定理求出BC即可;②等腰△ABC为钝角三角形时,求出BD,由勾股定理求出BC即可.
作CD⊥AB于D,
则∠ADC=∠BDC=90°,△ABC的面积=![]() ABCD=
ABCD=![]() ×10×CD=30,
×10×CD=30,
解得:CD=6,
∴AD=![]() =8m;
=8m;
分两种情况:
①等腰△ABC为锐角三角形时,如图1所示: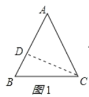
BD=ABAD=2m,
∴BC=![]() =
=![]() ;
;
②等腰△ABC为钝角三角形时,如图2所示:
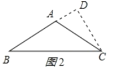
BD=AB+AD=18m,
∴BC=![]() =
=![]() ;
;
综上所述:BC的长为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目