题目内容
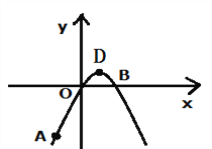
【题目】如图：在平面直角坐标系中，抛物线
经过A（—2，—4 ），O（0，0），B（2，0）三点.
（1）求抛物线
的解析式和顶点坐标D.
（2）若使
轴上一点P，使P 到A、D的距离之和最小，求P的坐标.
（3）若抛物线对称轴上一点M，使AM + OM最小，求AM + OM的最小值.
【答案】（1）
，D（1， 
）；（2）P（
，0）；（3）
.
【解析】试题分析：
（1）由抛物线
过点O（0，0），B（2，0）可设其解析式为
，再代入点A（-2，-4 ），可解得
的值，从而可得抛物线的解析式；
把所得解析式配方化为顶点式，即可得到顶点坐标；
（2）根据“两点之间线段最短”连接AD交
轴于点P，点P即为所求点；由A、D的坐标求出直线AD的解析式，就可求得点P的坐标；
（3）由题意可知，点O、B关于抛物线的对称轴对称，因此连接AB交抛物线对称轴于点M，则M为所求点，线段AB的长度就是OM+AM的最小值；根据A、B两点长坐标由两点间距离公式计算出AB的长度即可.
试题解析：
（1）抛物线
经过O（0，0），B（2，0），
则抛物线可设为
，由抛物线过点A（-2，-4 ）可得： 
, 解得： 
抛物线解析式为： 
即： 
，
配方得： 
，
∴抛物线的顶点D的坐标为：（1， 
）；
（2）连接AD交x轴于点P,
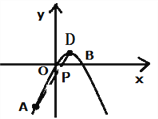
设直线AD的解析式为： 
，
∵D的坐标为：（1， 
），A的坐标为：（-2，-4 ），
∴有：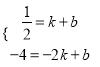 
，解得：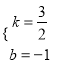 
，
∴直线AD为： 
.
当y=0时， 
，
解得x =
∴ P的坐标为： 
；
（3）由（1）知：抛物线为： 
∴对称轴为：直线为
∵点O与点B关于直线为
对称，连接AB交直线为
于M，
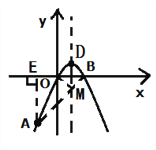
∴点M为所求点，连接MO，则MO+MA的最小值就是AB的长.
∵点A的坐标为： 
，点B的坐标为： 
，
∴AB=
，
∴AM + OM的最小值为
.
练习册系列答案
相关题目
