Question

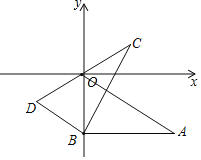
【题目】Rt△ABO与Rt△CBD在平面直角坐标系中的位置如图所示，∠ABO＝∠CBD＝90°，若点A（2，﹣2），∠CBA＝60°，BO＝BD，则点C的坐标是（　　）

A. （2，2）B. （1，）C. （，1）D. （2，2）

Answer 1

【答案】C

【解析】

过点C作CE垂直x轴于点E．先证明△ODB为等边三角形，求出OD、DB长，然后根据∠DCB＝30°，求出CD的长，进而求出OC，最后求出OE，CE，即求出点C坐标．

.解：如图，过点C作CE垂直x轴于点E．

∵A（2，﹣2），

∴OB＝2，AB＝2，

∵∠ABO＝∠CBD＝90°，

∴∠DBO＝∠CBA＝60°，

∵BO＝BD，

∴∠D＝DOB＝60°，

DO＝DB＝BO＝2，

∴∠BCD＝30°，

CD＝2BD＝4，

∴CO＝CD﹣OD＝4﹣2＝2，

∵∠COE＝90°﹣∠COy＝90°﹣60°＝30°

∴CE＝OC＝1，OE＝，

∴C（，1）．

故选：C．