��Ŀ����
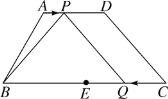
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����ABC��60�㣬AB��8��BC��16��AD��6.E��BC���е㣬��P��ÿ��1����λ���ȵ��ٶȴӵ�A��������AD���D�˶�����Qͬʱ��ÿ��2����λ���ȵ��ٶȴӵ�C��������CB���B�˶�����Pֹͣ�˶�ʱ����QҲ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮
(1)���BPQ�����ΪS����S��t֮��ĺ�����ϵʽ��
(2)��t��________ʱ����BPQ��������ı���PQCD�������ȣ�
(3)��tΪ��ֵʱ���Ե�P��Q��E��DΪ������ı�����ƽ���ı��Σ�
���𰸡�(1) S=��4![]() t��32
t��32![]() (0��t��6)�� (2)
(0��t��6)�� (2)![]() ��(3) 2��
��(3) 2��![]() ��
��
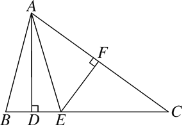
��������(1)����A��AF��BC�ڵ�F�����AFB��90�����ɺ�30��ǵ�ֱ�������ε����ʼ����ɶ����õ�AF�ij������������ε������ʽ���ɵõ����ۣ�
(2)��S��S�ı���PQCD ��S�ı���ABCD��S��BPQ��S��ABP����ʾ�������ֵ���������빫ʽ�ⷽ�̼��ɣ�
(3)����������������ı���PEQD���ı���PQEDΪƽ���ı��Σ��õ�PD��EQ��
��PD��6��t��EQ��8��2t��2t��8������ⷽ�̼��ɣ�
(1)����A��AF��BC�ڵ�F�����AFB��90����
�ߡ�ABC��60�������BAF��30����
��AB��8����BF��![]() AB��4����AF��
AB��4����AF��![]() ��
��![]() ��
��
�߾���t���BQ��16��2t����S��![]() ��BQ��AF��
��BQ��AF��![]() ��(16��2t)��
��(16��2t)��![]() ����
����![]() t��
t��![]() (0��t��6)��
(0��t��6)��
(2)��ͼ��֪S�ı���PQCD��S�ı���ABCD��S��BPQ��S��ABP��
��AP��t����S��ABP��![]() AP��AF��
AP��AF��![]() ��
��
�֡�S�ı���ABCD��![]() AF(AD��BC)��
AF(AD��BC)��![]() ��
��![]() ��(6��16)��
��(6��16)��![]() ����S�ı���PQCD��
����S�ı���PQCD��![]() ��(��
��(��![]() t��
t��![]() )��
)��![]() ��
��![]() ��
��
��S��S�ı���PQCD����![]() ����
����![]() t��
t��![]() ����ã�t��
����ã�t��![]() ��
��
(3)�������֪�ı���PEQD���ı���PQEDΪƽ���ı��Σ���PD��EQ��
��PD��6��t��EQ��8��2t��2t��8����6��t��8��2t��6��t��2t��8����ã�t��2��t��![]() ��
��
�ʵ�t��2��![]() ʱ���Ե�P��Q��E��DΪ������ı�����ƽ���ı��Σ�
ʱ���Ե�P��Q��E��DΪ������ı�����ƽ���ı��Σ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�