题目内容
已知二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,0)、(2,0),且﹣2<x1<﹣1,与y轴正半轴的交点在(0,2)的下方,则下列结论:
①abc<0;②b2>4ac;③2a+b+1<0;④2a+c>0.
则其中正确结论的序号是
| A.①② | B.②③ | C.①②④ | D.①②③④ |
C。
【考点】二次函数图象与系数的关系,一元二次方程的判别式和根与系数的关系,不等式的性质
解析试题分析:作出示意图如图, 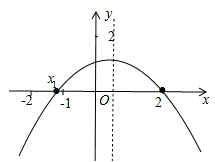
∵二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,0)、(2,0),且﹣2<x1<﹣1,与y轴正半轴相交,
∴a<0,c>0,对称轴在y轴右侧,则x=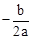 >0,
>0,
∴b>0。∴abc<0。所以①正确。
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,即b2>4ac。所以②正确。
当x=2时,y=0,即4a+2b+c=0,∴2a+b+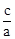 =0。
=0。
∵0<c<2,∴2a+b+1>0。所以③错误。
∵二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,0)、(2,0),
∴方程ax2+bx+c=0(a≠0)的两根为x1,2。∴2x1=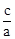 ,即x1=
,即x1= 。
。
∵﹣2<x1<﹣1,∴﹣2< <﹣1。
<﹣1。
∵a<0,∴﹣4a>c>﹣2a。∴2a+c>0。所以④正确。
综上所述,正确结论的序号是①②④。故选C。

练习册系列答案
相关题目
二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是
| A.a<0,b<0,c>0,b2﹣4ac>0 | B.a>0,b<0,c>0,b2﹣4ac<0 |
| C.a<0,b>0,c<0,b2﹣4ac>0 | D.a<0,b>0,c>0,b2﹣4ac>0 |
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是
| A.a>0 | B.3是方程ax2+bx+c=0的一个根 |
| C.a+b+c=0 | D.当x<1时,y随x的增大而减小 |
(2013年四川资阳3分)如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,﹣2),且顶点在第三象限,设P=a﹣b+c,则P的取值范围是【 】
| A.﹣4<P<0 | B.﹣4<P<﹣2 | C.﹣2<P<0 | D.﹣1<P<0 |
 的图象向左平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
的图象向左平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )


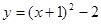
 (a<0)的图象上,则a的值为 ( )
(a<0)的图象上,则a的值为 ( )



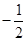

 的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .
的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .