题目内容
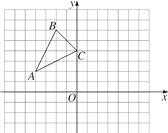
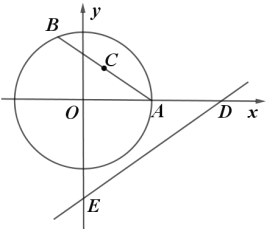
【题目】如图,在平面直角坐标系![]() 中,半径为2的
中,半径为2的![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,点
,点![]() 是
是![]() 上一动点,点
上一动点,点![]() 为弦
为弦![]() 的中点,直线
的中点,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,则
,则![]() 面积的最小值为________.
面积的最小值为________.
【答案】2
【解析】
如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.首先证明点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.求出MN,当点C与C′重合时,△C′DE的面积最小.
解:如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.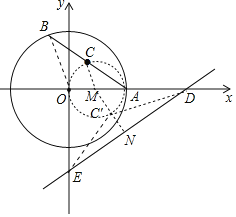
∵AC=CB,AM=OM,
∴MC=![]() OB=1,
OB=1,
∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.
∵直线y=![]() x-3与x轴、y轴分别交于点D、E,
x-3与x轴、y轴分别交于点D、E,
∴D(4,0),E(0,-3),
∴OD=4,OE=3,
∴![]() ,
,
∵∠MDN=∠ODE,∠MND=∠DOE,
∴△DNM∽△DOE,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
当点C与C′重合时,△C′DE的面积最小,△C′DE的面积最小值![]() ,
,
故答案为2.

练习册系列答案
相关题目