题目内容
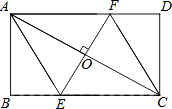
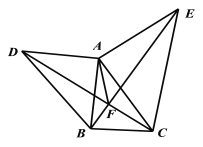
【题目】如图,在△ABC外分别以AB,AC为边作两个大小不同的等腰直角三角形ABD和等腰直角三角形ACE,其中∠DAB=∠CAE=90°,AB=AD,AC=AE.连结DCBE交于F点.
(1)请你找出一对全等的三角形,并加以证明;
(2)直线DC、BE是否互相垂直,请说明理由;
(3)求证:∠DFA=∠EFA.
【答案】(1)![]() ≌
≌![]() ,理由见解析;(2)
,理由见解析;(2)![]() ,理由见解析;(3)见解析.
,理由见解析;(3)见解析.
【解析】
(1)由题意可得AD=AB,AC=AE,由∠DAB=∠CAE=90°,可得到∠DAC=∠BAE,从而可证△DAC≌△BAE;
(2)由(1)可得∠ACD=∠AEB,再利用直角三角形的性质及等量代换即可得到结论;
(3)作AM⊥DC于M,AN⊥BE于N,利用全等三角形的面积相等及角平分线的判定即可证得结论.
(1)![]() ≌
≌![]() ,
,
理由是: ∵![]()
![]()
∴![]()
即![]()
又∵![]() ,
,![]()
∴![]() ≌
≌![]()
(2)![]() ,
,
理由是:
∵![]() ≌
≌![]()
∴![]()
∵![]()
![]()
∴![]()
∴![]()
∴![]()
(3)作![]() 于
于![]() ,
,![]() 于
于![]()
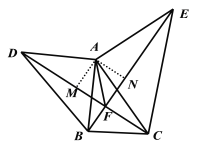
∵![]() ≌
≌![]()
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]() 是
是![]() 的平分线,
的平分线,
即![]() .
.

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案【题目】某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是( )
班级 | 1班 | 2班 | 3班 | 4班 | 5班 | 6班 |
人数 | 52 | 60 | 62 | 54 | 58 | 62 |
A.平均数是58
B.中位数是58
C.极差是40
D.众数是60
【题目】水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?