Question

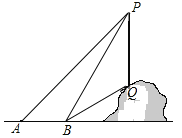
【题目】如图，为了测量山坡上一棵树PQ的高度，小明在点A处利用测角仪测得树顶P的仰角为45°，然后他沿着正对树PQ的方向前进10m到达点B处，此时测得树顶P和树底Q的仰角分别是60°和30°．

（1）求∠BPQ的度数；

（2）求树PQ的高度．

Answer 1

【答案】（1）30°；（2）10+．

【解析】

（1）延长PQ交直线AB于点C，根据直角三角形两锐角互余求得即可；

（2）设PC＝x，在直角△APC和直角△BPC中，根据三角函数利用x表示出AC和BC，根据AB＝AC﹣BC即可列出方程求得x的值，再在直角△BQC中利用三角函数求得QC的长，则PQ的长度即可求解．

延长PQ交直线AB于点C，（1）∠BPQ＝90°﹣60°＝30°；

（2）设PC＝x．在直角△APC中，∠PAC＝45°，则AC＝PC＝x；

∵∠PBC＝60°，∴∠BPC＝30°．

在直角△BPC中，BCPCx．

∵AB＝AC﹣BC＝10，∴xx＝10，解得：x＝15+5．

则BC＝55．

在直角△BCQ中，QCBC（55）＝5，∴PQ＝PC﹣QC＝15+5（5）＝10．

答：树PQ的高度为（10）m．