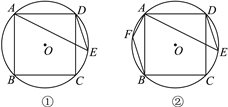题目内容
【题目】已知如图,是腰长为![]() 的等腰直角三角形
的等腰直角三角形![]() ,要求在其内部作出一个半圆,直径在
,要求在其内部作出一个半圆,直径在![]() 的边上,且半圆的弧与
的边上,且半圆的弧与![]() 的其他两边相切,则该半圆的半径是________(结果保留根号).
的其他两边相切,则该半圆的半径是________(结果保留根号).

【答案】![]() 或
或![]()
【解析】
分两种情况:①是直径在斜边上;②是直径在腰上分别求解半圆半径的长即可.
解:①∵半圆的直径在△ABC的斜边上,且半圆的弧与△ABC的两腰相切,切点为D、E,
如图1,连接OD,OA,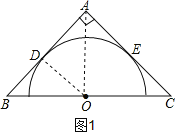
∵AB与⊙O相切,
∴OD⊥AB,
∵在等腰直角三角形ABC中,AB=AC=4,O为BC的中点,
∴AO⊥BC,
∴OD∥AC,
∵O为BC的中点,
∴OD=![]() AC=2.
AC=2.
②∵半圆的直径在△ABC的腰上,且半圆的弧与△ABC的斜边相切,切点为D,
如图2,连接OD,设半圆的半径为r,
∴OB=4-r,
∵在等腰直角三角形ABC中,AB=AC=4,
∴∠B=45°,
∴△OBD是等腰直角三角形,
∴OD=BD=r,
∴2r2=(4-r)2,解得r=-4+4![]() ,r=-4-4
,r=-4-4![]() (舍去),
(舍去),
故答案为:![]() 或
或![]()

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案【题目】某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点.从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
C | D | 总计/t | |
A | 200 | ||
B | x | 300 | |
总计/t | 240 | 260 | 500 |
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求
总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有3,4,5,x,甲,乙两人每次同时从袋中各随机取出1个小球,并计算2个小球上的数字之和.记录后将小球放回袋中搅匀,进行重复试验,试验数据如下表:
摸球总 次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为8”出 现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为8”出 现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果试验继续进行下去,根据上表提供的数据,出现和为8的频率将稳定在它的概率附近,估计出现和为8的概率是________;
(2)如果摸出的2个小球上数字之和为9的概率是,那么x的值可以为7吗?为什么?
【题目】在一个不透明的口袋里装有颜色不同的红、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 38 | 51 | 76 | 195 | 324 | 401 |
摸到白球的频率 | 0.38 | 0.34 | 0.38 | 0.39 | 0.405 | 0.401 |
(1)请估计:当n很大时,摸到白球的频率将会接近_______;(精确到0.1)
(2)试估算口袋中白球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;摸到两只白球的概率是多少?