题目内容
如图,梯形ABCD中,AD∥BC,BC=20cm,AD=10cm,现有两个动点P、Q分别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10)。
小题1:当t为何值时,四边形PCDQ为平行四边形?
小题2:在P、Q移动的过程中,线段PH的长是否发生改变?如果不变,求出线段PH的长;如果改变,请说明理由。
小题1:当t为何值时,四边形PCDQ为平行四边形?
小题2:在P、Q移动的过程中,线段PH的长是否发生改变?如果不变,求出线段PH的长;如果改变,请说明理由。

小题1:∵AD∥BC,BC=20cm,AD=10cm,点P、Q分别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,
∴DQ=t,PC=20-2t,
∵若四边形PCDQ为平行四边形,则DQ=PC,
∴20-2t=t,解得:t=
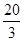 ;
;小题2:线段PH的长不变,
∵AD∥BH,P、Q两点的速度比为2:1,∴QD:BP=1:2,
∴QE:EP=ED:BE=1:2,
∵EF∥BH,∴ED:DB=EF:BC=1:3,
∵BC=20,∴EF=
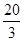 ,∴
,∴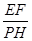 :
: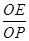 =
= 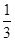 ,∴PH=20cm.
,∴PH=20cm.(1)平行四边形的两组对边分别相等;
(2)求得PH的长是一个定值,即长度不变。
(2)求得PH的长是一个定值,即长度不变。

练习册系列答案
相关题目
 于E,
于E, 于F,BD与AE、AF分别相交于G、H.
于F,BD与AE、AF分别相交于G、H. ,求证:四边形ABCD是菱形.
,求证:四边形ABCD是菱形.
 相交于点
相交于点 ,
, ,若要使□ABCD为矩形,则
,若要使□ABCD为矩形,则 的长应该为( ).
的长应该为( ).
 ,求四边形ABCD的周长.
,求四边形ABCD的周长.
 ABCD的一边BC延长至E,若∠A=110°,则∠1=________.
ABCD的一边BC延长至E,若∠A=110°,则∠1=________. [
[


