题目内容

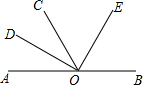
（推理填空）如图所示，点O是直线AB上一点，∠BOC=130°，OD平分∠AOC．求：∠COD的度数．
解：∵O是直线AB上一点
∴∠AOB=______．
∵∠BOC=130°
∴∠AOC=∠AOB-∠BOC=______．
∵OD平分∠AOC
∴∠COD=
1
2
______=______．
∵O是直线AB上一点
∴∠AOB=180°．
∵∠BOC=130°
∴∠AOC=∠AOB-∠BOC=50°．
∵OD平分∠AOC
∴∠COD=
1
2
∠AOC=25°．
故答案为180°、50°、∠AOC、25°．
练习册系列答案
相关题目
已知∠AOB=90°，∠COD=90°，画出示意图并探究∠AOC与∠BOD的关系．
如图，将一副三角板的直角顶点重合，摆放在桌面上．若∠AOD=150°，则∠BOC=______°．
将一副三角板如图摆放，若∠BAE=140°，则∠CAD的度数是______．
如图，在直线MN上，过点O在MN的同侧引射线OA、OB．若∠AOM=2∠AOB，且∠BON比∠AOB少16°，则∠AOB=______度，∠BON=______度．
将一副三角尺按如图方式叠在一起，三角尺的3个角的顶点是A、C、D，记作“三角尺ACD”；三角尺的3个角的顶点是E、C、B，记作“三角尺ECB”，且∠ACD=∠ECB=90°，∠A=60°，∠D=30°，∠E=∠B=45°．
（1）若∠ACB=140°，求∠DCE的度数；
（2）比较∠ACE与∠DCB的大小，并说明理由；
（3）三角尺ACD不动，将三角尺BCE的CE边与CA边重合，然后绕点C按顺时针方向任意转动一个角度，当∠ACE等于多少度时（0°＜∠ACE＜90°），这两块三角尺各有一条边所在的直线互相垂直，请直接写出∠ACE所有可能的值，不必说明理由．（提示：三角形内角和为180°．）
著名数学教育家G．波利亚，有句名言：“发现问题比解决问题更重要”，这句话启发我们：要想学好数学，就需要观察，发现问题，探索问题的规律性东西，要有一双敏锐的眼睛．请先观察、计算再填空．
已知：如图，OM平分∠AOB，ON平分∠BOC．
（1）当∠AOC=90°，∠BOC=70°时，∠MON=______；
（2）当∠AOC=80°，∠BOC=60°时，∠MON=______；
（3）当∠AOC=70°，∠BOC=50°时，∠MON=______；
（4）猜想：不论∠AOC和∠BOC的度数是多少，∠MON的度数总等于______度数的一半．
如图，点O在直线AB上，OD平分∠AOC，OE平分∠BOC，且∠AOD=30゜，求∠BOE的度数．
如图，已知∠AOC=90°，∠COB=α，OD平分∠AOB，则∠COD等于（　　）
A．
α
2
B．45°-
α
2
C．45°-αD．90°-α

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网