题目内容
【题目】已知:△ABC(如图),
(1)求作:作△ABC的内切圆⊙I.(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明).
(2)在题(1)已经作好的图中,若∠BAC=88°,求∠BIC的度数.
【答案】(1)作图见解析;(2)134°.
【解析】
试题(1)分别作出∠BAC、∠ABC的平分线,两平分线的交点即为△ABC的内切圆的圆心I,过点I向BC作垂线,垂足为H,垂足与I之间的距离即为⊙I的半径,以I为圆心,IH为半径画圆即可;
(2)先根据三角形内角和定理求出∠ABC+∠ACB的度数,再根据角平分线的性质得出∠IBC+∠ICB的度数,由三角形内角和定理即可求解.
试题解析:(1)①以A为圆心任意长为半径画圆,分别交AC、AB于点H、G;
②分别以H、G为圆心,以大于![]() HG为半径画圆,两圆相交于K点,连接AK,则AK即为∠BAC的平分线;
HG为半径画圆,两圆相交于K点,连接AK,则AK即为∠BAC的平分线;
③同理作出∠ABC的平分线BF,交AK于点I,则I即为△ABC内切圆的圆心;
④过I作IH⊥BC于H,以I为圆心,IH为半径画,则⊙I即为所求圆.
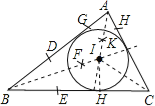
(2)∵∠BAC=88°,
∴∠ABC+∠ACB=180°-88°=92°,
∴∠IBC+∠ICB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×92°=46°,
×92°=46°,
∴∠BIC=180°-46°=134°.
考点: 三角形的内切圆与内心.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目