题目内容
【题目】已知点A、B、C、D在⊙O上，AB∥CD，AB=24，CD=10，⊙O的半径为13，求梯形ABCD的面积．
【答案】解：如图1所示：过点O作OE⊥CD，OF⊥AB， 且EF必过点O，
∵AB∥CD，AB=24cm，CD=10cm，圆O的直径为26cm，
∴EC=5cm，BF=12cm，
∴EO=12cm，FO=5cm，
则EF=17cm，
故梯形ABCD的面积为： 
（10+24）×17=289（cm2），
如图2，同理可得出：EF=12﹣5=7（cm），
则梯形ABCD的面积为： （10+24）×7=119（cm2）．
综上所述：梯形ABCD的面积为289cm2或119cm2 ．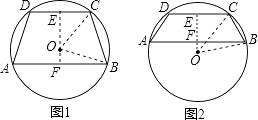 
【解析】根据题意画出图形，进而分类讨论得出EF的长，进而求出面积即可．
【考点精析】掌握梯形的定义是解答本题的根本，需要知道一组对边平行，另一组对边不平行的四边形是梯形．两腰相等的梯形是等腰梯形．
练习册系列答案
智能训练练测考系列答案
相关题目
