��Ŀ����
����Ŀ���ۺ���ʵ�����ı�����ת�е���ѧ
���ǻ�����ѧС���ڿ�����ѧ����о���һ�����⣬������ǽ��
����һ����ͼ1���ھ���ABCD�У�AB=6��AD=8��E��F�ֱ�ΪAB��AD�ߵ��е㣬�ı���AEGFΪ���Σ�����CG��
��1����ֱ��д��CG�ij���______��
��2����ͼ2��������AEGF�Ƶ�A��ת������˳ʱ����ת������G���ڱ�AB��ʱ�������DF��CG�ij���ͨ�����㣬�Բ���DF��CG֮���������ϵ��
��3��������AEGF�Ƶ�A��ת����ͼ3��λ��ʱ����2����DF��CG֮���������ϵ�Ƿ�������˵�����ɣ�
����������ǻ�����ѧС���ͼ�ε���ת��������չ�о�����ͼ4����ABCD�У���B=60�㣬AB=6��AD=8��E��F�ֱ�ΪAB��AD�ߵ��е㣬�ı���AEGFΪƽ���ı��Σ�����CG�����ǻ�����ѧС�鷢��DF��CG��Ȼ�������ض���������ϵ��
��4����ͼ5����AEGF�Ƶ�A��ת������˳ʱ����ת����������������ʱ�����ǻ�����ѧС�鷢��DF��CG��Ȼ��������һ�ض���������ϵ������ֱ��д������ض���������ϵ��





���𰸡�5
��������
��1����ͼ1�У��ɴ�EG��CD��H�����ı���FGHD�Ǿ��Σ���Rt��CGH�У����ù��ɶ������ɽ�����⣻
��2����ͼ2�У���FP��AD��P�����ù��ɶ������������ε����ʣ��ֱ����CG��DF���ɽ�����⣻
��3������������AG��AC��ֻҪ֤����ADF�ס�ACG���ɵ�![]() ���ɽ�����⣻
���ɽ�����⣻
��4����ͼ4�У�ͨ�����㼴�ɽ�����⣻
��1����ͼ1�У��ɴ�EG��CD��H�����ı���FGHD�Ǿ��Σ�
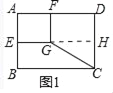
��Rt��CGH��GH=DF=4��CH=DH=AE=3��
��CG=![]() =5��
=5��
�ʴ�Ϊ��5��
��2����ͼ2�У���FP��AD��P��
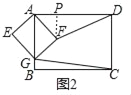
�ھ���AEGF�У���AE=3��EG=4��
��AG=5��BG=AB-AG=1��
��Rt��CBG��CG=![]() ��
��
����APF�ס�AEG���ɵ�![]() ��
��
��![]() ��
��
��AP=![]() ��PF=
��PF=![]() ��DP=AD��AP=8��
��DP=AD��AP=8��![]() ��
��
��Rt��PDF��DF=![]()
![]() ��
��
��DF=![]() CG��
CG��
��3���������������£�����AG��AC��
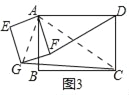
����ת��֪����DAF=��CAG��
�ɹ��ɶ�����֪��AC=![]() ��AG=5��
��AG=5��
��![]() ��
��![]() ��
��
��![]() ��
��
���ADF�ס�ACG��
��![]() ��
��
��DF=![]() CG��
CG��
��4����ͼ4�У��ӳ�EG��CD��H����CK��GH��K��
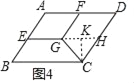
�������֪�ı���FGHD��ƽ���ı��Σ��ı���AEGF��ƽ���ı��Σ�
��DF=GH=4��DH=FG=AE=3��CH=3����CHG=��D=60�㣬
��Rt��CHK��HK=![]() ��CK=
��CK=![]() ��GK=GH��KH=
��GK=GH��KH=![]() ��
��
��Rt��CGK��CG= ![]() ��
��
��CG=![]() DF��
DF��
��ͼ5�У�����AG��AC��
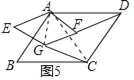
ͬ����֤����ACG�ס�ADF���ɵã�![]() =
=![]() ���ɵ�CG=
���ɵ�CG=![]() DF��
DF��