题目内容
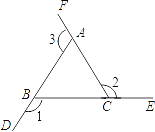
【题目】如图，射线AD，BE，CF构成∠1，∠2，∠3，则∠1+∠2+∠3=（ ）
A. 180° B. 360° C. 540° D. 无法确定
【答案】B
【解析】
由三角形的一个外角等于与它不相邻的两个内角的和,得∠1=∠BAC+∠BCA，∠2=∠ABC+∠BAC,∠3=∠ACB+∠ABC,所以∠1+∠2+∠3=2（∠BAC+∠BCA+∠ABC）,进而利用三角形的内角和定理求解．
解:∵∠1=∠BAC+∠BCA,∠2=∠ABC+∠BAC，∠3=∠ACB+∠ABC （三角形的一个外角等于与它不相邻的两个内角的和）,
∴∠1+∠2+∠3=2（∠BAC+∠BCA+∠ABC）,
又∵∠BAC+∠BCA+∠ABC=180° （三角形内角和定理）,
∴∠1+∠2+∠3=2×180°=360°.
故选B．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
