ЬтФПФкШн
ЁОЬтФПЁПAЁЂBСНГЧЯрОр600ЧЇУзЃЌвЛСОПЭГЕДгAГЧПЊЭљBГЧЃЌГЕЫйЮЊУПаЁЪБ80ЧЇУзЃЌЭЌЪБвЛСОГізтГЕДгBГЧПЊЭљAГЧЃЌГЕЫйЮЊАаЁЪБ100ЧЇУзЃЌЩшПЭГЕГіЪБМфЮЊtЃЎ ![]()
ЃЈ1ЃЉЁОЬНОПЁП ШєПЭГЕЁЂГізтГЕОрBГЧЕФОрРыЗжБ№ЮЊy1ЁЂy2 ЃЌ аДГіy1ЁЂy2ЙигкtЕФКЏЪ§ЙиЯЕЪНЃЌВЂМЦЫуЕБy1=200ЧЇУзЪБy2ЕФЃЎ
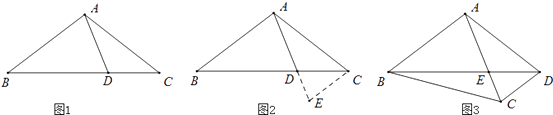
ЃЈ2ЃЉЁОЗЂЯжЁП ЩшЕуCЪЧAГЧгыBГЧЕФжаЕуЃЌ
ЃЈЂёЃЉФФИіГЕЛсЯШЕНДяCЃПИУГЕЕНДяCКѓдйОЙ§ЖрЩйаЁЪБЃЌСэвЛИіГЕЛсЕНДяCЃП
ЃЈЂђЃЉШєСНГЕПлЯрОр100ЧЇУзЪБЃЌЧѓЪБМфtЃЎ
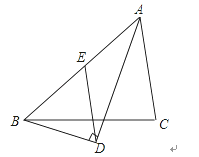
ЃЈ3ЃЉЁООіВпЁП МКжЊПЭГЕКЭГізтГЕе§КУдкAЃЌBжЎМфЕФЗўЮёеОDДІЯргіЃЌДЫЪБГізтГЕГЫПЭаЁЭѕЭЛШЛНгЕНПЊЛсЭЈжЊЃЌашвЊСЂМДЗЕЛиЃЌДЫЪБаЁЭѕгаСНжжбЁдёЗЕЛиBГЧЕФЗНАИЃК
ЗНАИвЛЃКМЬајГЫзјГізтГЕЃЌЕНДяAГЧКѓСЂПЬЗЕЛиBГЧЃЈЩшГізтГЕЕїЭЗЪБМфКіТдВЛМЦЃЉЃЛ
ЗНАИЖўЃКГЫзјПЭГЕЗЕЛиГЧЃЎ
ЪдЭЈЙ§МЦЫуЃЌЗжЮіаЁЭѕбЁдёФФжжЗНЪНФмИќПьЕНДяBГЧЃП
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКгЩвбжЊЃЌЕУy1=Љ80t+600ЃЌ
Сюy1=0ЃЌМДЉ80t+600=0ЃЌНтЕУt= ![]() ЃЌ
ЃЌ
ЙЪy1=Љ80t+600ЃЈ0ЁмtЁм ![]() ЃЉЃЎ
ЃЉЃЎ
y2=100tЃЌ
Сюy2=600ЃЌМД100t=600ЃЌНтЕУt=6ЃЌ
ЙЪy2=100tЃЈ0ЁмtЁм6ЃЉЃЎ
ЕБy1=200ЪБЃЌМД200=Љ80t+600ЃЌНтЕУt=5ЃЌ
ЕБt=5ЪБЃЌy2=100ЁС5=500ЃЎ
ЙЪЕБy1=200ЧЇУзЪБy2ЕФЮЊ500ЃЎ
ЃЈ2ЃЉНтЃКЃЈЂёЃЉЁп100ЃО60ЃЌ
ЁрГізтГЕЯШЕНДяCЃЎ
ПЭГЕЕНДяCЕуашвЊЕФЪБМфЃК600Љ80t1= ![]() ЃЌНтЕУt1=
ЃЌНтЕУt1= ![]() ЃЛ
ЃЛ
ГізтГЕЕНДяCЕуашвЊЕФЪБМфЃК100t2= ![]() ЃЌНтЕУt2=3ЃЎ
ЃЌНтЕУt2=3ЃЎ
![]() Љ3=
Љ3= ![]() ЃЈаЁЪБЃЉЃЎ
ЃЈаЁЪБЃЉЃЎ
ЫљвдГізтГЕЕНДяCКѓдйОЙ§ ![]() аЁЪБЃЌПЭГЕЛсЕНДяCЃЎ
аЁЪБЃЌПЭГЕЛсЕНДяCЃЎ
ЃЈЂђЃЉСНГЕЯрОр100ЧЇУзЃЌЗжСНжжЧщПіЃК
Ђйy1Љy2=100ЃЌМД600Љ80tЉ100t=100ЃЌ
НтЕУЃКt= ![]() ЃЛ
ЃЛ
Ђкy2Љy1=100ЃЌМД100tЉЃЈ600Љ80tЃЉ=100ЃЌ
НтЕУЃКt= ![]() ЃЎ
ЃЎ
злЩЯПЩжЊЃКСНГЕЯрОр100ЧЇУзЪБЃЌЪБМфtЮЊ ![]() Лђ
Лђ ![]() аЁЪБЃЎ
аЁЪБЃЎ
ЃЈ3ЃЉНтЃКСНГЕЯргіЃЌМД80t+100t=600ЃЌНтЕУt= ![]() ЃЌ
ЃЌ
ДЫЪБAD=80ЁС ![]() =
= ![]() ЃЈЧЇУзЃЉЃЌBD=600Љ
ЃЈЧЇУзЃЉЃЌBD=600Љ ![]() =
= ![]() ЃЈЧЇУзЃЉЃЎ
ЃЈЧЇУзЃЉЃЎ
ЗНАИвЛЃКt1=ЃЈ ![]() +600ЃЉЁТ100=
+600ЃЉЁТ100= ![]() ЃЈаЁЪБЃЉЃЛ
ЃЈаЁЪБЃЉЃЛ
ЗНАИЖўЃКt2= ![]() ЁТ80=
ЁТ80= ![]() ЃЈаЁЪБЃЉЃЎ
ЃЈаЁЪБЃЉЃЎ
Ёпt1ЃОt2ЃЌ
ЁрЗНАИЖўИќПь
ЁОНтЮіЁПЬНОПЃКИљОнТЗГЬ=ЫйЖШЁСЪБМфЃЌМДПЩЕУГіy1ЁЂy2ЙигкtЕФКЏЪ§ЙиЯЕЪНЃЌИљОнЙиЯЕЪНЫуГіy1=200ЧЇУзЪБЕФЪБМфtЃЌНЋtДњШыy2ЕФНтЮіЪНжаМДПЩЕУГіНсТлЃЛЗЂЯжЃКЃЈЂёЃЉИљОнГізтГЕЕФЫйЖШДѓгкПЭГЕЕФЫйЖШПЩЕУГіГізтГЕЯШЕНДяCЕуЃЌЬзгУЃЈ1ЃЉжаЕФКЏЪ§ЙиЯЕЪНЃЌСюy=300МДПЩЗжБ№ЫуГіЪБМфt1КЭt2 ЃЌ ЖўепзіВюМДПЩЕУГіНсТлЃЛЃЈ2ЃЉСНГЕЯрОр100ЧЇУзЃЌЗжСНжжЧщПіПМТЧЃЌНтЙигкtЕФвЛдЊвЛДЮЗНГЬМДПЩЕУГіНсТлЃЛОіВпЃКИљОнЪБМф=ТЗГЬЁТЫйЖШКЭЃЌЫуГіЕНДяЕуDЕФЪБМфЃЌдйИљОнТЗГЬ=ЫйЖШЁСЪБМфЫуГіADЁЂBDЕФГЄЖШЃЌНсКЯЪБМф=ТЗГЬЁТЫйЖШЃЌМДПЩЧѓГіСНжжЗНАИИїашЕФЪБМфЃЌСНепНјааБШНЯМДПЩЕУГіНсТлЃЎ