题目内容
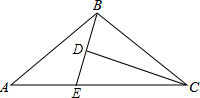
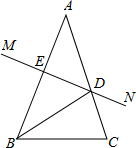
如图AB=AC,∠A=36°,AB的垂直平分线MN交AC于点D,交AB于E.
①求∠DBC的度数.
②猜想△BDC的形状并证明.
①求∠DBC的度数.
②猜想△BDC的形状并证明.

①∵DE是AB的垂直平分线,
∴AD=BD,
∴∠A=∠ABD=36°,
∵AC=AB,
∴∠C=∠ABC=
(180°-∠A)=72°,
∴∠DBC=∠ABC-∠ABD=72°-36°=36°,
答:∠DBC的度数是36°.
②△BDC的形状是等腰三角形,
证明:∵∠DBC=36°,∠C=72°,
∴∠BDC=180°-∠C-∠DBC=72°,
∴∠C=∠BDC,
∴BD=CB,
即△BDC是等腰三角形.
∴AD=BD,
∴∠A=∠ABD=36°,
∵AC=AB,
∴∠C=∠ABC=
| 1 |
| 2 |
∴∠DBC=∠ABC-∠ABD=72°-36°=36°,
答:∠DBC的度数是36°.
②△BDC的形状是等腰三角形,
证明:∵∠DBC=36°,∠C=72°,
∴∠BDC=180°-∠C-∠DBC=72°,
∴∠C=∠BDC,
∴BD=CB,
即△BDC是等腰三角形.

练习册系列答案
相关题目