题目内容
【题目】如图,正方形ABCD的边长为5,E是AB上一点,且BE:AE=1:4,若P是对角线AC上一动点,则PB+PE的最小值是 . (结果保留根号) 
【答案】![]()
【解析】解:连接BD, 则点D即为点B关于AC的对称点,连接DE交AC于点P,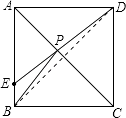
由对称的性质可得,PB=PD,故PE+PB=DE,
由两点之间线段最短可知,DE即为PE+PB的最小值,
∵AB=AD=5,BE:AE=1:4
∴BE=1,AE=4,
在Rt△ADE中,
DE= ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.

练习册系列答案
相关题目
【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
请根据所给信息,解答下列问题: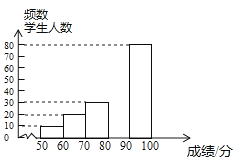
(1)a= , b=
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?

