题目内容
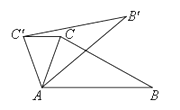
【题目】如图,在△ABC中,AB=AC,点D,E分别在边BC 和AC上,若AD=AE,则下列结论错误的是( ) 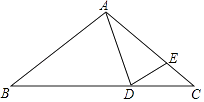
A.∠ADB=∠ACB+∠CAD
B.∠ADE=∠AED
C.∠CDE= ![]() ∠BAD
∠BAD
D.∠AED=2∠ECD
【答案】D
【解析】解:∵∠ADB是△ACD的外角,
∴∠ADB=∠ACB+∠CAD,选项A正确;
∵AD=AE,
∴∠ADE=∠AED,选项B正确;
∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠ADE+∠CDE=∠B+∠BAD,∠AED=∠CDE+∠C,
∴∠CDE+∠C+∠CDE=∠B+∠BAD,
∴∠CDE= ![]() ∠BAD,选项C正确;
∠BAD,选项C正确;
∵∠AED=∠ECD+∠CDE,∠ECD≠∠CDE,
∴选项D错误;
故选:D.
【考点精析】根据题目的已知条件,利用等腰三角形的性质的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角).

练习册系列答案
相关题目