Question

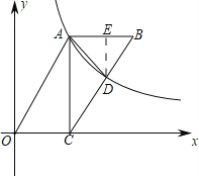
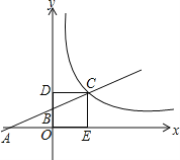
【题目】如图，直线y1=kx+1分别交x轴，y轴于点A．B，交反比例函数y2=（x＞0）的图象于点C，CD⊥y轴于点D，CE⊥x轴于点E，S△OAB=1，=．

（1）点A的坐标为______；

（2）求直线和反比例函数的解析式；

（3）根据图象直接回答：在第一象限内，当x取何值时，y1≥y2．

Answer 1

【答案】（1）（-2，0）；（2）y1=x+1；y2=；（3）x≥3时，y1≥y2．

【解析】

（1）先根据直线解析式求出OB长度，再根据面积求出OA长度，即可得A点坐标；

（2）把A点坐标代入直线y1=kx+1中求出k值就能得到直线解析式；由△AOB∽△AEC，得到比例式求出CE．OE长，从而根据C点坐标得到m值，即得反比例函数解析式；

（3）观察图象上下位置即可求解．

解：（1）当x=0时，y=kx+1=1，即OB=1．

∵S△OAB=1，∴OA=2．

∴A点的坐标为（-2，0）．

故答案为（-2，0）；

（2）把A（-2，0）代入y1=kx+1，得k=．

∴直线解析式为y1=x+1．

∵=

∴

∵OB∥CE，

∴△AOB∽△AEC．

∴．所以CE=，OE=3，

∴点C坐标为（3，）．

∴m=3×=7.5=．

∴反比例函数解析式为y2=．

（3）从图象可看出当x≥3时，y1≥y2．