题目内容
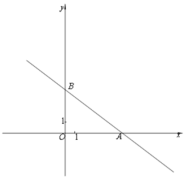
【题目】已知二次函数![]() 的图象与y轴的交点为C,与x轴正半轴的交点为A,且tan∠ACO=
的图象与y轴的交点为C,与x轴正半轴的交点为A,且tan∠ACO=![]() .
.
(1)求二次函数的解析式;
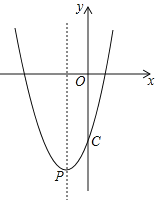
(2)P为二次函数图象的顶点,Q为其对称轴上的一点,QC平分∠PQO,求Q点坐标;
(3)是否存在实数![]() 、
、![]() (
(![]() ),当
),当![]() 时,y的取值范围为
时,y的取值范围为![]() ?若存在,直接写在
?若存在,直接写在![]() 、
、![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ;(2)Q(
;(2)Q(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)
);(3)![]() ,
,![]() .
.
【解析】
试题(1)由tan∠ACO=![]() ,求出OA的值,即可得出A点的坐标;然后把A点的坐标代入
,求出OA的值,即可得出A点的坐标;然后把A点的坐标代入![]() ,求出b的值,即可得出二次函数的解析式.
,求出b的值,即可得出二次函数的解析式.
(2)由Q为抛物线对称轴上的一点,设点Q的坐标为(![]() ,n);然后根据∠OQC=∠CQP、∠CQP=∠OCQ,可得∠OQC=∠OCQ,所以OQ=OC,据此求出n的值,进而得出Q点坐标即可.
,n);然后根据∠OQC=∠CQP、∠CQP=∠OCQ,可得∠OQC=∠OCQ,所以OQ=OC,据此求出n的值,进而得出Q点坐标即可.
(3)根据题意,分三种情况:①当![]() 时;②当
时;②当![]() 时;③当
时;③当![]() 时;然后根据二次函数的最值的求法,求出满足题意的实数
时;然后根据二次函数的最值的求法,求出满足题意的实数![]() 、
、![]() (
(![]() ),当
),当![]() 时,y的取值范围为
时,y的取值范围为![]() 即可.
即可.
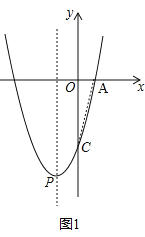
试题解析:(1)如图1,连接AC,
 ,
,
∵二次函数![]() 的图象与y轴的交点为C,∴C点的坐标为(0,﹣4),∵tan∠ACO=
的图象与y轴的交点为C,∴C点的坐标为(0,﹣4),∵tan∠ACO=![]() ,∴
,∴![]() ,又∵OC=4,∴OA=1,∴A点的坐标为(1,0),把A(1,0)代入
,又∵OC=4,∴OA=1,∴A点的坐标为(1,0),把A(1,0)代入![]() ,可得0=1+b﹣4,解得b=3,∴二次函数的解析式是:
,可得0=1+b﹣4,解得b=3,∴二次函数的解析式是:![]() ;
;
(2)如图2,
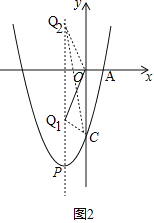 ,
,
∵![]() ,
,
∴抛物线的对称轴是:![]() ,∵Q为抛物线对称轴上的一点,∴设点Q的坐标为(
,∵Q为抛物线对称轴上的一点,∴设点Q的坐标为(![]() ,n),∵抛物线的对称轴平行于y轴,∴∠CQP=∠OCQ,又∵∠OQC=∠CQP,∴∠OQC=∠OCQ,∴OQ=OC,∴
,n),∵抛物线的对称轴平行于y轴,∴∠CQP=∠OCQ,又∵∠OQC=∠CQP,∴∠OQC=∠OCQ,∴OQ=OC,∴![]() ,∴
,∴![]() ,解得n=
,解得n=![]() ,∴Q点坐标是(
,∴Q点坐标是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
(3)①当![]() 时,二次函数
时,二次函数![]() 单调递减,∵y的取值范围为
单调递减,∵y的取值范围为![]() ,∴
,∴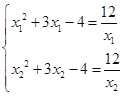 ,由
,由![]() ,解得
,解得![]() =﹣3,﹣2,2,由
=﹣3,﹣2,2,由![]() ,解得
,解得![]() =﹣3,﹣2,2,∵
=﹣3,﹣2,2,∵![]() ,∴
,∴![]() ;
;
②当![]() 时,
时,
Ⅰ、当![]() 时,可得
时,可得![]() ,∵y的取值范围为
,∵y的取值范围为![]() ,
,
∴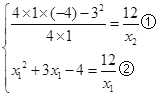 ,由①,可得
,由①,可得![]() ,由②,可得
,由②,可得![]() =﹣3,﹣2,2,∵
=﹣3,﹣2,2,∵![]() ,
,![]() ,∴没有满足题意的
,∴没有满足题意的![]() 、
、![]() ;
;
Ⅱ、当![]() 时,可得
时,可得![]() ,∵y的取值范围为
,∵y的取值范围为![]() ,
,
∴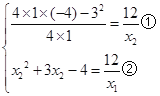 ,解得:
,解得: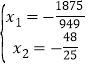 ,∵
,∵![]() ≈﹣1.98﹣1.92=﹣3.9<﹣3,∴没有满足题意的
≈﹣1.98﹣1.92=﹣3.9<﹣3,∴没有满足题意的![]() 、
、![]() .
.
③当![]() 时,二次函数
时,二次函数![]() 单调递增,∵y的取值范围为
单调递增,∵y的取值范围为![]() ,∴
,∴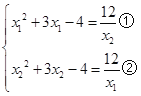 ,①×
,①×![]() ﹣②×
﹣②×![]() ,可得:
,可得:![]() ,∵
,∵![]() ≠0,∴
≠0,∴![]() =0,∴
=0,∴![]() ③,把③代入①,可得:
③,把③代入①,可得:![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴没有满足题意的
,∴没有满足题意的![]() 、
、![]() .
.
综上,可得:![]() ,
,![]() ,当
,当![]() 时,y的取值范围为
时,y的取值范围为![]() .
.

 名校课堂系列答案
名校课堂系列答案