题目内容
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,下列结论错误的是
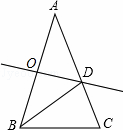

| A.∠C=2∠A | B.BD平分∠ABC |
| C.S△BCD=S△BOD | D.点D为线段AC的黄金分割点 |
C
试题分析:A、∵∠A=36°,AB=AC,∴∠C=∠ABC=72°,
∴∠C=2∠A,正确,故本选项错误。
B、∵DO是AB垂直平分线,∴AD=BD。
∴∠A=∠ABD=36°。∴∠DBC=72°﹣36°=36°=∠ABD。
∴BD是∠ABC的角平分线,正确,故本选项错误。
C,根据已知不能推出△BCD的面积和△BOD面积相等,错误,故本选项正确。
D、∵∠C=∠C,∠DBC=∠A=36°,∴△DBC∽△CAB。
∴
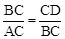 ,即BC2=BC•AC。
,即BC2=BC•AC。∵∠C=72°,∠DBC=36°,∴∠BDC=72°=∠C。∴BC=BD。
∵AD=BD,∴AD=BC。
∴AD2=CD•AC,即点D是AC的黄金分割点,正确,故本选项错误。
故选C。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
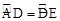 ,AB=5,BD=4,则sin∠ECB= .
,AB=5,BD=4,则sin∠ECB= .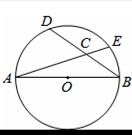
 、
、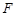 ,若
,若 ,则
,则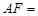 .
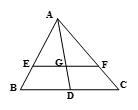
.
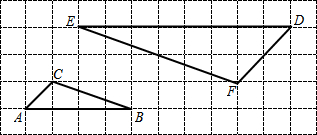
 的值为 ;
的值为 ;