Question

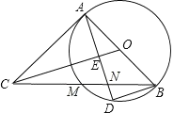
【题目】如图，AB是⊙O的直径，CA与⊙O相切于点A，且CA＝BA．连接OC，过点A作AD⊥OC于点E，交⊙O于点D，连接DB．

（1）求证：△ACE≌△BAD；

（2）连接CB交⊙O于点M，交AD于点N．若AD＝4，求MN的长．

Answer 1

【答案】（1）证明见解析；（2） ．

【解析】

（1）由直径AB，得∠ADB=∠AEC=90°，再证明∠CAE=∠ABD，最后全等三角形的判定定理得结论；
（2）连接AM，求得AD=DE的长度，由勾股定理求得AB、BC的长度，再由△CEN∽△BDN求得BN，再由勾股定理求得BM的长度，便可求得MN．

（1）证明：∵AB是⊙O的直径，
∴∠ADB=90°，
∵AD⊥OC，
∴∠AEC=90°，
∴∠ADB=∠AEC，
∵CA是⊙O的切线，
∴∠CAO=90°，
∴∠ACE=∠BAD，
在△ACE和△BAD中，
，
∴△ACE≌△BAD（AAS）；
（2）解：连接AM，如图，

∵AD⊥OC，AD=4，
∴AE=DE=AD=2，
∵△ACE≌△BAD，
∴BD=AE=2，CE=AD=4，
在Rr△ABD中，AB=，
在Rt△ABC中，BC=，
∵∠CEN=∠BDN=90°，∠CNE=∠BND，
∴△CEN∽△BDN，
∴＝2，
∴BN= ，
∵AB是⊙O的直径，
∴∠AMB=90°，即AM⊥CB，
∵CA=BA，∠CAB=90°，
∴BM=BC=，
∴MN=BM-BN= ．