题目内容
平行四边形的底增加
,底上的高减少
,新的平行四边形的面积比原来增加了 .
| 2 |
| 5 |
| 1 |
| 4 |
考点:平行四边形的面积,百分数的实际应用
专题:平面图形的认识与计算
分析:因为设原来的平行四边形的底是a,高是h,根据平行四边形的面积=底×高,计算出原来的平行四边形的面积,增加后的底是(1+
)a,减少后的高为(1-
)h,根据平行四边形的面积计算公式计算出后来的面积,进行比较,得出结论.
| 2 |
| 5 |
| 1 |
| 4 |
解答:
解:设原来的平行四边形的底是a,高是h,则增加后的底是(1+
)a,减少后的高为(1-
)h:
原来的平行四边形的面积是:ah
变化后的平行四边形的面积是:(1+
)a×(1-
)h=
ah
(
ah-ah)÷ah
=
ah÷ah
=
答:新的平行四边形的面积比原来增加了
.
故答案为:
.
| 2 |
| 5 |
| 1 |
| 4 |
原来的平行四边形的面积是:ah
变化后的平行四边形的面积是:(1+
| 2 |
| 5 |
| 1 |
| 4 |
| 21 |
| 20 |
(
| 21 |
| 20 |
=
| 1 |
| 20 |
=
| 1 |
| 20 |
答:新的平行四边形的面积比原来增加了
| 1 |
| 20 |
故答案为:
| 1 |
| 20 |
点评:解答此题的关键是先设出原来平行四边形的底和高,进而根据平行四边形的面积计算方法求出原来的长方形的面积;分别计算出后来平行四边形的底与高,并计算出后来的面积,进行比较,得出结论.

练习册系列答案
相关题目
 按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2厘米和4厘米,乙三角形两条直角边分别为3厘米和6厘米,求图中阴影部分的面积.
按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2厘米和4厘米,乙三角形两条直角边分别为3厘米和6厘米,求图中阴影部分的面积. 如图,在三角形ABC中,AB、AC两边分别被分成五等份.阴影部分的面积与空白部分的面积比是
如图,在三角形ABC中,AB、AC两边分别被分成五等份.阴影部分的面积与空白部分的面积比是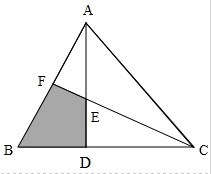 已知△ABC的面积为24cm2,D为BC中点,E为AD中点,求阴影部分面积.
已知△ABC的面积为24cm2,D为BC中点,E为AD中点,求阴影部分面积.