题目内容
 直角三角形ABC中,∠ABC=90.,AB=20厘米,以AB为直径的半圆与直角三角形ABC的重叠部分用阴影表示,不重叠的两部分甲和乙,甲的面积比乙的面积大75平方厘米,求直角边BC的长.
直角三角形ABC中,∠ABC=90.,AB=20厘米,以AB为直径的半圆与直角三角形ABC的重叠部分用阴影表示,不重叠的两部分甲和乙,甲的面积比乙的面积大75平方厘米,求直角边BC的长.分析:根据题意,先求出半圆面积,由“甲的面积比乙的面积大75平方厘米”可知半圆面积比三角形ABC的面积大75平方厘米,然后求出半圆面积,设BC=x,表示出三角形ABC的面积,列方程解答问题.
解答:解:半圆面积:
3.14×(20÷2)2÷2,
=3.14×100÷2,
=157(平方厘米);
设BC=x,三角形ABC的面积:
20x÷2=10x;
因为甲的面积比乙的面积大75平方厘米,也就是半圆面积比三角形ABC的面积大75平方厘米,所以:
157-10x=75,
10x=82,
x=8.2;
答:直角边BC的长是8.2厘米.
3.14×(20÷2)2÷2,
=3.14×100÷2,
=157(平方厘米);
设BC=x,三角形ABC的面积:
20x÷2=10x;
因为甲的面积比乙的面积大75平方厘米,也就是半圆面积比三角形ABC的面积大75平方厘米,所以:
157-10x=75,
10x=82,
x=8.2;
答:直角边BC的长是8.2厘米.
点评:此题灵活运用了圆的面积以及三角形的面积公式,跟据数量关系,列出等式,解决问题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 (1)量出右图直角三角形各边上的长(结果取整厘米数),并填在图中相应的括号里.
(1)量出右图直角三角形各边上的长(结果取整厘米数),并填在图中相应的括号里. 如图,在直角三角形ABC中,AB=4cm,AC=3cm,BC=5cm?
如图,在直角三角形ABC中,AB=4cm,AC=3cm,BC=5cm? 如图,直角三角形ABC中,AB长10厘米,∠C=45°,求图中阴影部分的面积.
如图,直角三角形ABC中,AB长10厘米,∠C=45°,求图中阴影部分的面积. 如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为
如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为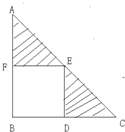 如图,在直角三角形ABC中有一个正方形BDEF,E点正好落在直角三角形的斜边AC上,已知AE=10厘米,EC=8厘米,则阴影部分的面积是多少平方厘米?
如图,在直角三角形ABC中有一个正方形BDEF,E点正好落在直角三角形的斜边AC上,已知AE=10厘米,EC=8厘米,则阴影部分的面积是多少平方厘米?