题目内容
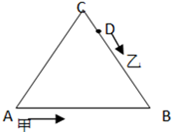 如图,等边三角形ABC周长为360米,D是BC上一点,CD=30米,甲从A点出发每分钟走55米,逆时针前进,乙从D点顺时针出发,每分钟行50米.问:两个人同时出发,几分钟相遇?当乙到达A时,甲在哪条边上,离乙多远?
如图,等边三角形ABC周长为360米,D是BC上一点,CD=30米,甲从A点出发每分钟走55米,逆时针前进,乙从D点顺时针出发,每分钟行50米.问:两个人同时出发,几分钟相遇?当乙到达A时,甲在哪条边上,离乙多远?分析:等边三角形ABC周长为360米,则每条边长360÷3=120米,所以DB长是120-30=90米,则A到B到D全长120+90=210米,又两人的速度是50+55米,则用ABD的长度除以两人的速度和,即得几人钟相遇.
当乙到达A时,乙已行了210÷50=4.2分钟,则甲行了55×4.2=231米,120+120=240米>231米,即此时甲在BC边上,距乙231米.
当乙到达A时,乙已行了210÷50=4.2分钟,则甲行了55×4.2=231米,120+120=240米>231米,即此时甲在BC边上,距乙231米.
解答:解:(360÷3+360÷3-30)÷(55+50)
=(120+120-30)÷105
=210÷105
=2(分钟)
(360÷3+360÷3-30)÷50×55
=210÷50×55
=213(米)
120+120=240>231
答:两个人同时出发,2钟相遇,当乙到达A时,甲在BC,离乙231米.
=(120+120-30)÷105
=210÷105
=2(分钟)
(360÷3+360÷3-30)÷50×55
=210÷50×55
=213(米)
120+120=240>231
答:两个人同时出发,2钟相遇,当乙到达A时,甲在BC,离乙231米.
点评:根据等边三角形的性质求出每条边的长度,进而求出ACD的长度是完成本题的关键.

练习册系列答案
相关题目
 如图中由等边三角形ABO,AOD,DOC围成的等腰梯形,它的面积是1,又知M是AB的中点,那么△COM面积等于多少?
如图中由等边三角形ABO,AOD,DOC围成的等腰梯形,它的面积是1,又知M是AB的中点,那么△COM面积等于多少?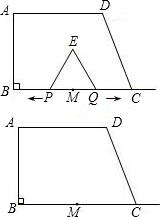
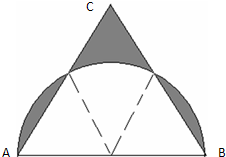 已知等边三角形ABC,边长是6厘米,以AB为直径画半圆(如图),求阴影部分的面积.(π取3.14)
已知等边三角形ABC,边长是6厘米,以AB为直径画半圆(如图),求阴影部分的面积.(π取3.14) 如图,已知△ABD与△BCD都是边长为3厘米的等边三角形,以A为圆心,AB长为半径画弧BD;以B为圆心,BC长为半径画弧CD,求阴影部分图形的周长.
如图,已知△ABD与△BCD都是边长为3厘米的等边三角形,以A为圆心,AB长为半径画弧BD;以B为圆心,BC长为半径画弧CD,求阴影部分图形的周长.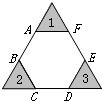 如图,六边形ABCDEF的各边都相等,每个内角都是120°,AB、CD、EF每两条线的延长线交于一点,三个交点构成一个等边三角形,若阴影部分的面积和是S,则六边形ABCDEF的面积为
如图,六边形ABCDEF的各边都相等,每个内角都是120°,AB、CD、EF每两条线的延长线交于一点,三个交点构成一个等边三角形,若阴影部分的面积和是S,则六边形ABCDEF的面积为