题目内容
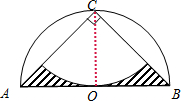
图中直角三角形ABC的面积是24平方厘米，求阴影部分面积．
分析：观察图形可知，阴影部分的面积等于三角形ABC的面积减去中间空白处的
圆的面积；因为半圆的半径与中间的
圆的半径相等，设这个半径是r厘米，则根据三角形ABC的面积是24平方厘米可得：2r×r÷2=24，据此即可得出r2=24，代入圆的面积公式求出这个
圆的面积即可解答问题．
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答：解：设这个半径是r厘米，则根据三角形ABC的面积是24平方厘米可得：
2r×r÷2=24，可得出r2=24，
24-3.14×24×
=24-18.84
=5.16（平方厘米）
答：阴影部分的面积是5.16平方厘米．
2r×r÷2=24，可得出r2=24，
24-3.14×24×
| 1 |
| 4 |
=24-18.84
=5.16（平方厘米）
答：阴影部分的面积是5.16平方厘米．
点评：主要考查了不规则图形的面积的计算方法，一般都是把不规则图形转化为规则图形中利用面积公式计算解答．
练习册系列答案
相关题目
（2011?广州模拟）如图，直角三角形ABC中，AB是圆的直径，且AB=20厘米，如果阴影a的面积比阴影b的面积大7平方厘米，BC的长度是
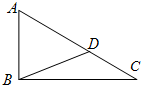如图，直角三角形ABC中，∠ABC=90°，∠ACB=30°，点D在AC上，如果∠ADB=45°，那么∠ABD=