题目内容
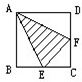 正方形ABCD的边长是8厘米,它的内部有一个三角形AEF(如图),线段DF=3.6厘米,BE=2.8厘米,那么三角形AEF的面积等于
正方形ABCD的边长是8厘米,它的内部有一个三角形AEF(如图),线段DF=3.6厘米,BE=2.8厘米,那么三角形AEF的面积等于26.96
26.96
平方厘米.分析:①阴影部分的面积=正方形的面积-(△ABE的面积+△ADF的面积+△ECF的面积);
②DF=3.6厘米,BE=2.8厘米,所以可得:CF=8-3.6=4.4(厘米),CE=8-2.8=5.2(厘米),由此可以求得这三个三角形的面积之和为:
×(3.6×8+2.8×8+4.4×5.2)=37.04(平方厘米);所以阴影部分的面积=8×8-37.04=26.96(平方厘米).
②DF=3.6厘米,BE=2.8厘米,所以可得:CF=8-3.6=4.4(厘米),CE=8-2.8=5.2(厘米),由此可以求得这三个三角形的面积之和为:
| 1 |
| 2 |
解答:解:根据题干分析可得:
×(3.6×8+2.8×8+4.4×5.2),
=
×(28.8+22.4+22.88),
=
×74.08,
=37.04(平方厘米),
8×8-37.04,
=64-37.04,
=26.96(平方厘米),
答:阴影部分的面积是26.96平方厘米.
故答案为:26.96.
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=37.04(平方厘米),
8×8-37.04,
=64-37.04,
=26.96(平方厘米),
答:阴影部分的面积是26.96平方厘米.
故答案为:26.96.
点评:此题关键是将阴影部分的面积转化成求正方形的面积和周围三个直角三角形的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 图中正方形ABCD的边长是12厘米,DE的长是EC的2倍.求CF的长是多少厘米.
图中正方形ABCD的边长是12厘米,DE的长是EC的2倍.求CF的长是多少厘米. 如图,已知正方形ABCD的边长为10,若以A为圆心,10为半径,画扇形ABD;在扇形ABD内作⊙O与AD、AB、弧都相切,求⊙O的周长.
如图,已知正方形ABCD的边长为10,若以A为圆心,10为半径,画扇形ABD;在扇形ABD内作⊙O与AD、AB、弧都相切,求⊙O的周长. 如图,正方形ABCD的边长是4厘米,长方形EDGF的边EF过A点,G点在BC上,若DG=5厘米.求EDGF的宽DE是多少厘米?
如图,正方形ABCD的边长是4厘米,长方形EDGF的边EF过A点,G点在BC上,若DG=5厘米.求EDGF的宽DE是多少厘米?
 奥运会即将开幕了,全市掀起了美化城市的热潮.有位同学为一家商店设计了一副霓虹灯闪烁的原理图.
奥运会即将开幕了,全市掀起了美化城市的热潮.有位同学为一家商店设计了一副霓虹灯闪烁的原理图.