题目内容
如图所示,正方形ABCD的边长是12厘米,等腰三角形EFG的斜边EF长18厘米,C、E相距13厘米,正方形以每秒3厘米的速度向右运动,同时直角三角形以每秒2厘米的速度向左移动,运动5秒后,正方形与三角形重叠部分的面积是多少平方厘米?


分析:如图:

原来BE=BC+CE=12+13=25(厘米);
又因为(3+2)×5=25(厘米),所以B、E重合.
阴影部分的面积=大直角三角形的面积-小直角三角形的面积,
大直角三角形的面积=18×18÷4=81(平方厘米),
因此,重叠部分的面积是81-6×6÷2=63(平方厘米).

原来BE=BC+CE=12+13=25(厘米);
又因为(3+2)×5=25(厘米),所以B、E重合.
阴影部分的面积=大直角三角形的面积-小直角三角形的面积,
大直角三角形的面积=18×18÷4=81(平方厘米),
因此,重叠部分的面积是81-6×6÷2=63(平方厘米).
解答:解:BE=BC+CE=12+13=25(厘米);
又因为(3+2)×5=25(厘米),所以B、E重合.
因此,重叠部分的面积是:18×18÷4-6×6÷2=63(平方厘米).
答:正方形与三角形重叠部分的面积是63平方厘米.
又因为(3+2)×5=25(厘米),所以B、E重合.
因此,重叠部分的面积是:18×18÷4-6×6÷2=63(平方厘米).
答:正方形与三角形重叠部分的面积是63平方厘米.
点评:此题解答的关键是通过作图找出正方形与三角形之间的关系,进而解答问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形. 如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是
如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是 如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?
如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?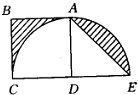 如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米?
如图所示,正方形ABCD,等腰三角形ADE,及半圆CAE,若AB=2厘米,则阴影部分的面积是多少平方厘米? 如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是________平方厘米.
如图所示,正方形ABCD的边长为10厘米,E、F分别为AB 及BC的中点.四边形BFGE的面积是________平方厘米.