Question

将图l的直角等腰三角形的两端如图2那样折起，再对折后可得到图3那样的图形，请问图3中阴影部分的面积是多少平方厘米？

Answer 1

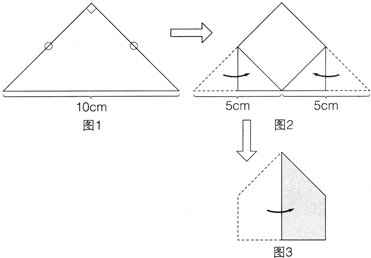
分析：折成的图3是一个直角梯形，下底是原等腰三角形斜边上的高，据等腰直角三角形的特征，斜边上的高是斜边的

1

2

；高是原等腰直角三角形斜边的

1

4

；根据三角形的中位线定理，上底是下底的

1

2

，根据梯形面积的面积公式S=（上底+下底）×高÷2即可求出阴影部分的面积．

解答：解：（10×

1

2

+10×

1

2

×

1

2

）×（10×

1

4

）÷2
=（5+2.5）×2.5÷2
=7.5×2.5÷2
=9.375（cm²）
答：阴影部分的面积是9.375cm²．

点评：本题是考查简单图形的折叠问题，折叠后是一个梯形，关键是弄清这个梯形的上、下底和高是多少．