题目内容
求1×2×3×…×2008×2009的计算结果中，末尾连续的“0”有多少个？
分析：根据题意，因为每一个5与每一个2相乘等于一个10即可得到末尾1个0，那么可利用分解质因数的方法将1到2009这些数中共含有几个因数5、几个因数2，因为分解质因数后2的个数要远远大于5的个数，所以有几个5就能形成几个10，也就是所求的几个0了，进行计算即可得到答案．
解答：解：在1-2009中，
是5的倍数的有：2009÷5=401（个），余数省略；
是25的倍数的有：2009÷25=80（个），余数省略；
是125的倍数的有：2009÷125=16（个），余数省略；
是625的倍数的有：2009÷625=3（个），余数省略，
所以5出现的次数就是401+80+16+3
=481+16+3，
=500（次），
所以在1至2009个数中共有500个因数5出现，
那么1×2×3×…×2008×2009积的末尾会有500个0出现．
答：1×2×3×…×2008×2009积的末尾连续的0会有500个．
是5的倍数的有：2009÷5=401（个），余数省略；
是25的倍数的有：2009÷25=80（个），余数省略；
是125的倍数的有：2009÷125=16（个），余数省略；
是625的倍数的有：2009÷625=3（个），余数省略，
所以5出现的次数就是401+80+16+3
=481+16+3，
=500（次），
所以在1至2009个数中共有500个因数5出现，
那么1×2×3×…×2008×2009积的末尾会有500个0出现．
答：1×2×3×…×2008×2009积的末尾连续的0会有500个．
点评：解答此题的关键是确定所有因数中有多少个质因数5出现，有几个质因数5积的末尾就会有几个连续的0出现．
练习册系列答案
相关题目
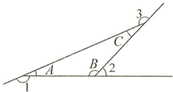如图，三角形三个内角分别为∠A、∠B、∠C，外角分别为∠1、∠2、∠3，已知：∠A+∠B+∠C=180°，∠A=∠C．