题目内容
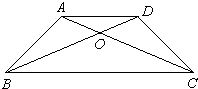在梯形ABCD中，上底长5厘米，下底长10厘米，S△BOC=20平方厘米，则梯形ABCD的面积是45
45
平方厘米．分析：因为AD∥BC，所以
=
=
，又AD=5厘米，BC=10厘米，所以
=
=
=2：1．然后利用三角形面积之间的关系，解决问题．
| AD |
| BC |
| AO |
| CO |
| DO |
| BO |
| AD |
| BC |
| A0 |
| CO |
| DO |
| BO |
解答：解：因为AD∥BC，所以
=
=
又AD=5厘米，BC=10厘米，所以
=
=
=2：1．
在△BOC与△DOC中，因其高相等，且
BO：DO=2：1，所以S△BOC：S△DOC=2：1
而 S△BOC=20cm2，所以S△DOC=10cm2．
同理，在△COD与△OAD中，因CO：AO=2：1，
且在相应边上的高相等，故：=2：1
即 S△AOD=
×10=5cm2．
在△AOB与BOC中，因AO：CO=1：2，且其在相应边上的高相等，故S△AOB：S△BOC=1：2．
即S△AOB=10cm2
综上，S梯形=S△AOB+S△BOC+S△COD+S△AOD
=10+20+10+5
=45cm2
故答案为：45．
| AD |
| BC |
| AO |
| CO |
| DO |
| BO |
又AD=5厘米，BC=10厘米，所以
| AD |
| BC |
| A0 |
| CO |
| DO |
| BO |
在△BOC与△DOC中，因其高相等，且
BO：DO=2：1，所以S△BOC：S△DOC=2：1
而 S△BOC=20cm2，所以S△DOC=10cm2．
同理，在△COD与△OAD中，因CO：AO=2：1，
且在相应边上的高相等，故：=2：1
即 S△AOD=
| 1 |
| 2 |
在△AOB与BOC中，因AO：CO=1：2，且其在相应边上的高相等，故S△AOB：S△BOC=1：2．
即S△AOB=10cm2
综上，S梯形=S△AOB+S△BOC+S△COD+S△AOD
=10+20+10+5
=45cm2
故答案为：45．
点评：此题考查了三角形的面积公式以及底一定时面积与高成正比的性质的灵活应用．
练习册系列答案
相关题目
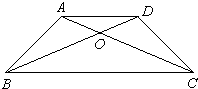
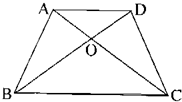在梯形ABCD中，上底长4厘米，下底长8厘米，S△COD=9平方厘米，梯形ABCD面积是
在梯形ABCD中，上底长4厘米，下底长8厘米，S△COD=9平方厘米，梯形ABCD面积是________．