题目内容
将1～8八个数分别填入下图的圈内，使三个大圆上的四个数的和都相等．这个和最大可以是多少？最小必须是多少？分析：要使和最小，重复数字尽可能要小．因为：1+2+3+…+8+a+a+b+c=3k（a、b、c为重复的数字，k为大圆上的四个数的和），也就是36+2a+b+c=3k，所以2a+b+c的和应是3的倍数，且尽可能小，只有1+1+3+4=9能被3整除且最小，36+9=3k，k=45÷3=15；同样，要使和最大，则考虑重复数字尽可能大，只有8+8+7+4=27能被3整除且最大，36+27=3k，k=63÷3=21．
解答：解：根据分析：这个和最大可以是21；最小必须是15．
填法如下图：
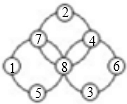
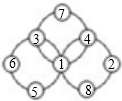
填法如下图：
点评：从图片以及数字特点入手，分析各圆上数的和，从重复数字入手，逐步分析，最后求出答案．
练习册系列答案
相关题目
将1至8八个数分别填入圈内，使每个大圆上五个数的和分别为20、21或22，一共各有几组填法？
