Question

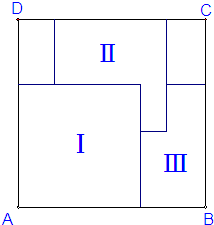如图，三个大小相同的正方形重叠地放在一个大的正方形ABCD内，已知能看见的部分Ⅰ、Ⅱ、Ⅲ的面积分别是64平方厘米、38平方厘米、34平方厘米．那么正方形ABCD的边长是

12.5

厘米．

Answer 1

分析：由题意得每个小正方形的边长都为8厘米，则将图Ⅱ所在的小正方形向左移动到最左边，则图Ⅱ减少的面积等于图Ⅲ增加的面积，图Ⅱ面积+图Ⅲ面积=38+34=72（平方厘米），如图

因为大正方形ABCD的边长=小正方形的边长+a=小正方形的边长+b，所以a=b，所以将图Ⅱ所在的小正方形向左移动到最左边后，图Ⅱ的面积为8b等于图Ⅲ的面积8a，则求出a或b的长度，大正方形ABCD的边长=8+a或b的长度，代数计算即可．

解答：解：如上图图所示：设出其中两条边分别为a，b：
则将图Ⅱ所在的小正方形向左移动到最左边，图Ⅱ减少的面积等于图Ⅲ增加的面积，
图Ⅱ面积+图Ⅲ面积=38+34=72（平方厘米），
因为大正方形ABCD的边长=小正方形的边长+a=小正方形的边长+b，所以a=b，
所以将图Ⅱ所在的小正方形向左移动到最左边后，图Ⅱ的面积等于图Ⅲ的面积，
即8a=8b=72÷2=36（平方厘米），
则a=b=36÷8=4.5（厘米），
则大正方形ABCD的边长为：8+4.5=12.5（厘米）．
答：正方形ABCD的边长是12.5厘米．
故答案为：12.5．

点评：此题考查了面积与等积变换的知识，解答本题的关键是发现把图Ⅱ向左移动，图Ⅱ减小的面积等于图Ⅲ增加的面积，这是突破口，难度较大．