题目内容
 在长方形ABCD中,AB=30厘米,BC=40厘米,P为BC上一点,PQ垂直为AC,PR垂直于BD.求PQ与PR的长度之和.
在长方形ABCD中,AB=30厘米,BC=40厘米,P为BC上一点,PQ垂直为AC,PR垂直于BD.求PQ与PR的长度之和.分析:如图所示,连接OP,则三角形OBC的面积就等于长方形的面积的
,又因S△OPB+S△OPC=S△OBC,且OB=OC=
DB,于是求出DB的长度,问题即可迎刃而解.

| 1 |
| 4 |
| 1 |
| 2 |

解答:解:长方形的面积:40×30=1200(平方厘米),
三角形OBC的面积:1200×
=300(平方厘米),
又因302+402=DB2,
900+1600=DB2,
DB2=2500,
所以DB=50(厘米),
因此OB=OC=50÷2=25(厘米),
所以
×25×PR+
×25×PQ=300,
×25×(PR+PQ)=300,
PR+PQ=300×2÷25,
=24(厘米);
答:PQ与PR的长度之和是24厘米.
三角形OBC的面积:1200×
| 1 |
| 4 |
又因302+402=DB2,
900+1600=DB2,
DB2=2500,
所以DB=50(厘米),
因此OB=OC=50÷2=25(厘米),
所以
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
PR+PQ=300×2÷25,
=24(厘米);
答:PQ与PR的长度之和是24厘米.
点评:解答此题的关键明白:三角形OBC的面积就等于长方形的面积的
,求出DB的长度,问题即可逐步得解.
| 1 |
| 4 |

练习册系列答案
相关题目
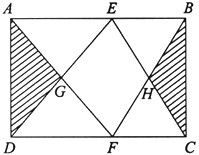 如图,在长方形ABCD中,AE=DF,已知阴影部分的面积是16cm2,四边形EGFH的面积是
如图,在长方形ABCD中,AE=DF,已知阴影部分的面积是16cm2,四边形EGFH的面积是 在长方形ABCD中,AB=120厘米,点Q以每秒3厘米的速度从A向B运动,点P以每秒4厘米的速度从C向D运动,两点同时运动多少秒后,P,Q的连线将长方形ABCD的面积分成3:5两部分?
在长方形ABCD中,AB=120厘米,点Q以每秒3厘米的速度从A向B运动,点P以每秒4厘米的速度从C向D运动,两点同时运动多少秒后,P,Q的连线将长方形ABCD的面积分成3:5两部分?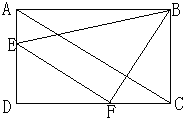 [“神奇‘的辅助线].在长方形ABCD中,EF平行AC,如果△BFC的面积是30平方厘米,那么△AEB的面积是多少平方厘米?
[“神奇‘的辅助线].在长方形ABCD中,EF平行AC,如果△BFC的面积是30平方厘米,那么△AEB的面积是多少平方厘米? 如图,在长方形ABCD中,以AB为轴旋转一周所形成的图形是
如图,在长方形ABCD中,以AB为轴旋转一周所形成的图形是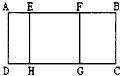 如图,在长方形ABCD中,EFGH是正方形.如果AF=16厘米,HC=21厘米,那么长方形ABCD的周长是
如图,在长方形ABCD中,EFGH是正方形.如果AF=16厘米,HC=21厘米,那么长方形ABCD的周长是