题目内容
 在图中,三角形DEF比三角形ABF面积小15平方厘米,求DE=?厘米.
在图中,三角形DEF比三角形ABF面积小15平方厘米,求DE=?厘米.分析:根据题意,三角形DEF比三角形ABF面积小15平方厘米,那么三角形BCE的面积比长方形ABCD的面积小15平方厘米,可利用长方形的面积公式减去15平方厘米就是三角形的BCE的面积,再根据三角形的面积公式计算出高CE的长,DE=CE-CD,列式解答即可得到答案.
解答:解:三角形BCE的面积为:4×10-15
=40-15,
=25(平方厘米),
三角形BCE的高CE为:25×2÷10
=50÷10,
=5(厘米),
DE的长为:5-4=1(厘米),
答:DE的长为1厘米.
=40-15,
=25(平方厘米),
三角形BCE的高CE为:25×2÷10
=50÷10,
=5(厘米),
DE的长为:5-4=1(厘米),
答:DE的长为1厘米.
点评:解答此题的关键是确定三角形BCE的面积比长方形ABCD的面积小15平方厘米,然后再计算三角形BCE的高CE的长,最后再计算DE的长即可.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图所示,两个等腰直角三角形ABC和DEF叠放在一起,如果BC=10,EF=8,CE=FC+BE,那么图中阴影部分的面积是
如图所示,两个等腰直角三角形ABC和DEF叠放在一起,如果BC=10,EF=8,CE=FC+BE,那么图中阴影部分的面积是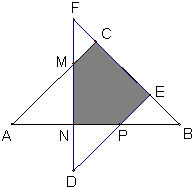 如图所示,两个等腰直角三角形ABC和DEF叠放在一起,如果BC=10,EF=8,CE=FC+BE,那么图中阴影部分的面积是________.
如图所示,两个等腰直角三角形ABC和DEF叠放在一起,如果BC=10,EF=8,CE=FC+BE,那么图中阴影部分的面积是________.